파이썬 정렬 알고리즘 모음 + 속도 테스트

15개 정렬 알고리즘 소개

0. 정렬 알고리즘 속도 테스트 코드

big-O-calculator 이용 @설치 링크

import bisect
import heapq
import inspect
from random import randint, shuffle
from statistics import mean
from timeit import default_timer, repeat

import matplotlib.pyplot as plt
from bigO import BigO
from win10toast import ToastNotifier


# timeit.repeat 이용
def runAlgorithm(algorithm, array, timeResults):
    setup_code = f"from __main__ import {algorithm}" if algorithm != "sorted" else ""

    stmt = f"{algorithm}({array})"

    times = repeat(setup=setup_code, stmt=stmt, repeat=3, number=5)
    timeResults[algorithm] = round(min(times), 5)

    print(f"def: {algorithm}(), 최소 실행 시간: {mean(times)/5:.5f}초")


# timeit.default_timer() 직접 계산
def runAlgorithm2(algorithm, array, timeResults):
    tot = 0.0
    # print("정렬 전", array)
    t0 = default_timer()
    if algorithm == "sorted":
        result = list(sorted(array))
    else:
        result = globals()[algorithm](array)
    t1 = default_timer()
    # print("정렬 후", result)
    print(f"{algorithm}() 정렬 결과 : {list(sorted(array)) ==  result}")
    tot += t1 - t0

    timeResults[algorithm] = round(tot, 5)
    print(f"def: {algorithm}(), 최소 실행 시간: {tot:.5f}초")


# 추천
def runAlgorithm3(algorithm, array, timeResults):
    lib = BigO()

    # print("정렬 전", array)

    testArray = array.copy()
    time, result = lib.runtime(algorithm, testArray, epoch=3, prtResult=False)  # 3회 평균

    print(f"{algorithm.__name__}(array) 정렬 결과 : {sorted(testArray) ==  result}")
    # print("정렬 후", result)

    timeResults[algorithm] = round(time, 5)
    
    
def retrieve_name(var):  # 변수 이름 가져오기
    callers_local_vars = inspect.currentframe().f_back.f_locals.items()
    return [var_name for var_name, var_val in callers_local_vars if var_val is var]


def saveResultAsPNG(timeResults, name, title):  # 그래프 저장
    times = []
    labels = []
    # 값에 따른 정렬
    for key, value in sorted(timeResults.items(), key=lambda x: x[1]):
        times.append(value)
        labels.append(key.__name__)

    plt.figure(figsize=(10, 8), dpi=80)  # 800x640

    ax = plt.subplot()
    ax.set_xticks(range(len(times)))
    ax.set_xticklabels(labels, rotation=20)

    plt.bar(range(len(times)), times)

    plt.title(f"{title} (length: {ARRAY_LENGTH})")
    plt.ylabel("Times (sec)")

    plt.savefig(name)


def switch(name):
    return {
        "array1": "Random",
        "array2": "Decending sorted",
        "array3": "Ascending sorted",
        "array4": "Partially sorted",
        "array5": "Ksorted",
        "array6": "All equal",
        "array7": "Almost equal",
        "array8": "Hole",
    }.get(name, "")


toaster = ToastNotifier()
toaster.show_toast("Sorting",
                   "Sorting algorithms are running",
                   icon_path="D:\DEV\Code\Python\img\python.ico",
                   duration=10)

# setrecursionlimit(ARRAY_LENGTH)

if __name__ == "__main__":
    lib = BigO()

    ARRAY_LENGTH = 5000  # 배열 크기
    
    # Random
    array1 = lib.genRandomArray(ARRAY_LENGTH)
    # Decending sorted
    array2 = lib.genReversedArray(ARRAY_LENGTH)
    # Ascending sorted
    array3 = lib.genSortedArray(ARRAY_LENGTH)
    # Partially sorted
    array4 = lib.genPartialArray(ARRAY_LENGTH)
    # Ksorted
    array5 = lib.genKsortedArray(ARRAY_LENGTH, ARRAY_LENGTH.bit_length())
    # Equal
    array6 = lib.genEqualArray(ARRAY_LENGTH)
    # Almost Equal
    array7 = lib.genAlmostEqualArray(ARRAY_LENGTH)
    # Hole
    array8 = lib.genHoleArray(ARRAY_LENGTH)

    # for 1, 2 run()
    times = {"sorted": 0, "countSort": 0, "introSort": 0,
             "timSort": 0, "quickSort": 0, "mergeSort": 0, "heapSort": 0,
             "smoothSort": 0,
             "pancakeSort": 0, "insertSort": 0, "bubbleSort": 0,
             "gnomeSort": 0}

    run = {
        sorted: 0,
        countSort: 0,
        introSort: 0,
        timSort: 0,
        quickSort2: 0,
        mergeSort: 0,
        heapSort: 0,
        smoothSort: 0,
        pancakeSort: 0,
        insertSort: 0,
        insertSort2: 0,
        binaryInsertSort: 0,
        bubbleSort: 0,
        goSort: 0,
    }

    test = [array1, array2, array3, array4, array5, array6, array7, array8]
    for index in range(len(test)):
        for function in run.keys():
            testArray = test[index].copy()  # Shallow Copy
            runAlgorithm3(algorithm=function, array=testArray, timeResults=run)

        name = switch(retrieve_name(test[index])[0])
        saveResultAsPNG(run3, f"array{index + 1}.png", name)

    # runAlgorithm(algorithm="bogoSort", array=testArray, timeResults=times)

    toaster.show_toast(
        "Sorting", "Measurements done", icon_path=None, duration=5, threaded=False
    )

1. Bubble Sort (버블 정렬)

def bubbleSort(array):  # in-place | stable
    """
    Best : O(n) | O(1) Space
    Average : O(n^2) | O(1) Space
    Worst : O(n^2) | O(1) Space
    """
    isSorted = False
    counter = 0
    n = len(array) - 1
    while not isSorted:
        isSorted = True
        for i in range(n - counter):
            if array[i] > array[i + 1]:
                array[i], array[i + 1] = array[i + 1], array[i]
                isSorted = False
                
        counter += 1
        
    return array

2. Binary Insertion Sort (바이너리 삽입 정렬)

def binarySearch(array, item, start, end):
    if start == end:
        if array[start] > item:
            return start
        else:
            return start + 1
    if start > end:
        return start

    mid = (start + end) // 2

    if array[mid] < item:
        return binarySearch(array, item, mid + 1, end)

    elif array[mid] > item:
        return binarySearch(array, item, start, mid - 1)
    else:
        return mid
        

def binaryInsertSort(array):
    for index in range(1, len(array)):
        value = array[index]
        pos = binarySearch(array, value, 0, index - 1)
        array = array[:pos] + [value] + \
            array[pos:index] + array[index + 1:]
    return array

3. Bogo Sort

def bogoSort(array):  # in-place
    """
    Best Case Complexity: O(n)
    Average Case Complexity: O(n(n-1)!)
    Worst Case Complexity: O(∞)
    """

    def is_sorted(array):
        i = 0
        while i+1 < len(array):
            if array[i] > array[i+1]:
                return False
            i += 1
        return True

    while not is_sorted(array):
        shuffle(array)

    return array

4. Brick Sort (Odd-Even Sort) 홀짝 정렬

def brickSort(array):
    """ Odd-Even Sort"""
    isSorted = False
    n = len(array) - 1
    while not isSorted:
        isSorted = True
        for i in range(1, n, 2):
            if array[i] > array[i + 1]:
                array[i], array[i + 1] = array[i + 1], array[i]
                isSorted = False

        for i in range(0, n, 2):
            if array[i] > array[i + 1]:
                array[i], array[i + 1] = array[i + 1], array[i]
                isSorted = False

    return array

5. Count Sort

def countSort(arr):  # stable
    # Time Complexity : O(n) | Space Complexity : O(n)
    minValue = min(arr)
    maxValue = max(arr) - minValue

    buckets = [0 for _ in range(maxValue + 1)]

    for i in arr:
        buckets[i - minValue] += 1

    index = 0
    for i in range(len(buckets)):
        while buckets[i] > 0:
            arr[index] = i + minValue
            index += 1
            buckets[i] -= 1

    return arr

6. Comb Sort (빗 정렬)

def combSort(array):
    gap = n = len(array)
    swapped = True

    while gap > 1 or swapped:
        swapped = False

        gap = int(gap * 10 / 13)

        if gap < 1:
            swapped = False
            gap = 1

        for i in range(n - gap):
            if array[i] > array[i + gap]:
                array[i], array[i + gap] = array[i + gap], array[i]
                swapped = True

    return array

7. Gnome Sort

def gnomeSort(array):  # in-place | stable
    '''
    Best : O(n) Time | O(1) Space
    Average : O(n^2) Time | O(1) Space
    Worst : O(n^2) Time | O(1) Space
    '''
    index = 0
    while index < len(array):
        if index == 0:
            index = index + 1
        if array[index] >= array[index - 1]:
            index = index + 1
        else:
            array[index], array[index-1] = array[index-1], array[index]
            index = index - 1

    return array

8. Heap Sort (힙 정렬)

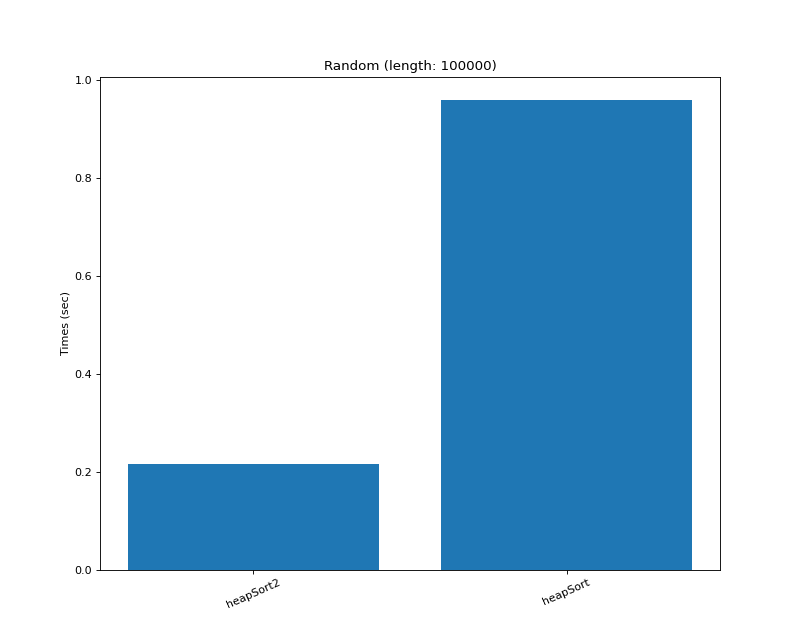
def heapSort(arr):  # in-place | not-stable
    # Time Complexity O(nlogn) | Space Complexity O(1)

    def heapify(arr, n, i):  # Max Heap
        largest = i  # 트리에서 가장 큰 값 찾기
        l = 2 * i + 1  # Left Node
        r = 2 * i + 2  # Right Node

        if l < n and arr[i] < arr[l]:
            largest = l

        if r < n and arr[largest] < arr[r]:
            largest = r

        # root가 최대가 아니면
        # 최대 값과 바꾸고, 계속 heapify
        if largest != i:
            arr[i], arr[largest] = arr[largest], arr[i]
            heapify(arr, n, largest)

    n = len(arr)

    for i in range(n // 2, -1, -1):
        heapify(arr, n, i)

    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        # Heapify root element
        heapify(arr, i, 0)

    return arr
    
    
# 파이썬 heappop, heapify 소스 이용
def heapSort2(iterable):  # in-place | not-stable
    # Time Complexity O(nlogn)
    # Using Python source at
    # https://github.com/python/cpython/blob/975d10a4f8f5d99b01d02fc5f99305a86827f28e/Lib/heapq.py

    def heappop(heap):
        """Pop the smallest item off the heap, maintaining the heap invariant."""
        lastelt = heap.pop()  # raises appropriate IndexError if heap is empty
        if heap:
            returnitem = heap[0]
            heap[0] = lastelt
            _siftup(heap, 0)
            return returnitem
        return lastelt

    def _siftup(heap, pos):
        endpos = len(heap)
        startpos = pos
        newitem = heap[pos]
        # Bubble up the smaller child until hitting a leaf.
        childpos = 2 * pos + 1  # leftmost child position
        while childpos < endpos:
            # Set childpos to index of smaller child.
            rightpos = childpos + 1
            if rightpos < endpos and not heap[childpos] < heap[rightpos]:
                childpos = rightpos
            # Move the smaller child up.
            heap[pos] = heap[childpos]
            pos = childpos
            childpos = 2 * pos + 1
        # The leaf at pos is empty now.  Put newitem there, and bubble it up
        # to its final resting place (by sifting its parents down).
        heap[pos] = newitem
        _siftdown(heap, startpos, pos)

    def _siftdown(heap, startpos, pos):
        newitem = heap[pos]
        # Follow the path to the root, moving parents down until finding a place
        # newitem fits.
        while pos > startpos:
            parentpos = (pos - 1) >> 1
            parent = heap[parentpos]
            if newitem < parent:
                heap[pos] = parent
                pos = parentpos
                continue
            break
        heap[pos] = newitem

    def heapify(x):
        """Transform list into a heap, in-place, in O(len(x)) time."""
        n = len(x)
        # Transform bottom-up.  The largest index there's any point to looking at
        # is the largest with a child index in-range, so must have 2*i + 1 < n,
        # or i < (n-1)/2.  If n is even = 2*j, this is (2*j-1)/2 = j-1/2 so
        # j-1 is the largest, which is n//2 - 1.  If n is odd = 2*j+1, this is
        # (2*j+1-1)/2 = j so j-1 is the largest, and that's again n//2-1.
        for i in reversed(range(n // 2)):
            _siftup(x, i)

        return x

    h = heapify(iterable)

    return [heappop(h) for _ in range(len(h))]

heapSort2를 파이썬 소스에서 따와서 사용해보았는데

전체적으로 heapSort2가 237% 가량 빠르다.

 

9. Insertion Sort (삽입 정렬)

def insertSort(array):  # in-place | stable
    '''
    Best O(n) Time | O(1) Space
    Average O(n^2) Time | O(1) Space
    Worst (On^2) Time | O(1) Space
    '''
    for i in range(len(array)):
        j = i
        toChange = array[i]
        while (j != 0 and array[j - 1] > toChange):
            array[j] = array[j - 1]
            j -= 1
        array[j] = toChange
    return array
    
    
# 좀 더 간단히
def insertSort(array):
    for i in range(1, len(array)):
        j = i
        
        while j > 0 and array[j] < array[j - 1]:
            array[j], array[j - 1] = array[j - 1], array[j]
            j -= 1
            
    return array

9-1. Insertion Sort 최적화

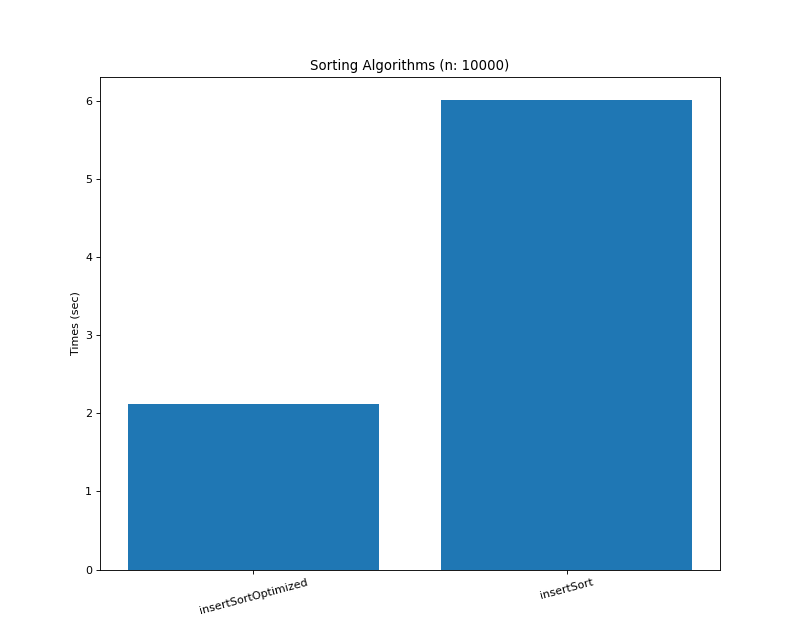
정렬된 케이스빼곤 3~5배 정도 빠름

def insertSortOptimized(array):
    for i in range(1, len(array)):
        if array[i] >= array[i - 1]:
            continue
        for j in range(i):
            if array[i] < array[j]:
                array[j], array[j + 1 : i + 1] = array[i], array[j:i]
                break

    return array

10. Introspective Sort (내성 정렬)

heap Sort + Insertion Sort + Quick Sort

https://choiseokwon.tistory.com/209

def introSort(array):  # in-place | not-stable
    # Time Complexity O(nlogn) | Space Complexity O(logn)
    maxDepth = 2 * (len(array).bit_length() - 1)
    sizeThreshold = 16
    return introSortHelper(array, 0, len(array), sizeThreshold, maxDepth)


def introSortHelper(array, start, end, sizeThreshold, depthLimit):
    def medianOf3(array, lowIdx, midIdx, highIdx):
        if (array[lowIdx] - array[midIdx]) * (array[highIdx] - array[lowIdx]) >= 0:
            return array[lowIdx]

        elif (array[midIdx] - array[lowIdx]) * (array[highIdx] - array[midIdx]) >= 0:
            return array[midIdx]

        else:
            return array[highIdx]

    def getPartition(array, low, high, pivot):
        i = low
        j = high
        while True:

            while (array[i] < pivot):
                i += 1
            j -= 1
            while (pivot < array[j]):
                j -= 1
            if i >= j:
                return i
            array[i], array[j] = array[j], array[i]
            i += 1

    while(end - start > sizeThreshold):
        if depthLimit == 0:
            return heapSort(array)
        depthLimit -= 1

        median = medianOf3(array, start, start +
                           ((end - start) // 2) + 1, end - 1)
        p = getPartition(array, start, end, median)
        introSortHelper(array, p, end, sizeThreshold, depthLimit)
        end = p

    return insertSort(array, start, end)
    
def insertSort(array, begin=0, end=None):  # in-place | stable
    '''
    Best O(n) Time | O(1) Space
    Average O(n^2) Time | O(1) Space
    Worst (On^2) Time | O(1) Space
    '''
    if end == None:
        end = len(array)
    for i in range(begin, end):
        j = i
        toChange = array[i]
        while (j != begin and array[j - 1] > toChange):
            array[j] = array[j - 1]
            j -= 1
        array[j] = toChange
    return array

11. Merge Sort (병합 정렬)

def mergeSort(array):  # stable
    """
    Best : O(nlogn) Time | O(n) Space
    Average : O(nlogn) Time | O(n) Space
    Worst : O(nlongn) Time | O(n) Space
    """

    def mergeHelper(main, startIdx, endIdx, aux):
        if startIdx == endIdx:
            return
        middleIdx = (startIdx + endIdx) // 2
        mergeHelper(aux, startIdx, middleIdx, main)
        mergeHelper(aux, middleIdx + 1, endIdx, main)
        merge(main, startIdx, middleIdx, endIdx, aux)

    def merge(main, startIdx, middleIdx, endIdx, aux):
        k = startIdx
        i = startIdx
        j = middleIdx + 1
        while i <= middleIdx and j <= endIdx:
            if aux[i] <= aux[j]:
                main[k] = aux[i]
                i += 1
            else:
                main[k] = aux[j]
                j += 1
            k += 1

        while i <= middleIdx:
            main[k] = aux[i]
            i += 1
            k += 1
        while j <= endIdx:
            main[k] = aux[j]
            j += 1
            k += 1

    if len(array) <= 1:
        return array

    aux = array[:]
    mergeHelper(array, 0, len(array) - 1, aux)
    return array

12. Pancake Sort (팬케이크 정렬)

def pancakeSort(array):  # in-place | not-stable
    # O(n^2) Time | O(N) Space
    if len(array) <= 1:
        return array
    for cur in range(len(array), 1, -1):
        # Finding index of maximum number in arr
        index_max = array.index(max(array[0:cur]))
        if index_max+1 != cur:
            # Needs moving
            if index_max != 0:
                # reverse from 0 to index_max
                array[:index_max+1] = reversed(array[:index_max+1])
            # Reverse list
            array[:cur] = reversed(array[:cur])
    return array

13. Quick Sort (빠른 정렬)

빠른 정렬은 pivot 선택 방식에 따라 속도 차이가 난다.

보통, low=0, mid=(high-low)//2, end=len(array) -1을 사용하지만, 이 방식은 정렬된 배열에서 속도가 매우 떨어진다.

최적화 방법1)

pivot 선택 랜덤 getMedian(randint[len(array)-1], randint[len(array)-1], randint[len(array)-1])

위 방식은, $1.2nlogn$ 비교를 하게 된다.

def quickSort(array):  # in-place | not-stable
    '''
    Best : O(nlogn) Time | O(logn) Space
    Average : O(nlogn) Time | O(logn) Space
    Worst : O(n^2) Time | O(logn) Space
    '''
    if len(array) <= 1:
        return array
    smaller, equal, larger = [], [], []
    pivot = array[randint(0, len(array)-1)]
    for x in array:
        if x < pivot:
            smaller.append(x)
        elif x == pivot:
            equal.append(x)
        else:
            larger.append(x)
    return quickSort(smaller)+equal+quickSort(larger)


# Hoare + Tail recursive + insertion sort
def quickSort2(array, low=0, high=None):
    def insertSort(array, low=1, high=None):
        if high is None:
            high = len(array)

        for i in range(low, high):
            j = i
            while j > 0 and array[j] < array[j - 1]:
                array[j], array[j - 1] = array[j - 1], array[j]
                j -= 1

        return array

    if high is None:
        high = len(array) - 1

    while low < high and high - low > 16:
        q = partition(array, low, high)
        quickSort2(array, low, q)
        low = q + 1

    return insertSort(array, low + 1, high + 1)


# Hoare's partition scheme
def partition(array, low, high):
    pivot = array[(high + low) // 2]
    # pivot = array[randint(low, high)]
    i = low - 1
    j = high + 1
    while True:
        i += 1
        while array[i] < pivot:
            i += 1
        j -= 1
        while array[j] > pivot:
            j -= 1

        if i >= j:
            return j

        array[i], array[j] = array[j], array[i]


# QuickSort 단순 버전
def quickSortSimple(arr):
    if len(arr) <= 1:
        return arr
    else:
        return quickSortSimple([x for x in arr[1:] if x < arr[0]]) + [arr[0]] + quickSortSimple([x for x in arr[1:] if x >= arr[0]])

14. Selection Sort (선택 정렬)

def selectionSort(array):  # in-place, unstable
    '''
    Best : O(n^2) Time | O(1) Space
    Average : O(n^2) Time | O(1) Space
    Worst : O(n^2) Time | O(1) Space
    '''
    for currentIdx in range(len(array) - 1):
        smallestIdx = currentIdx
        for i in range(currentIdx + 1, len(array)):
            if array[smallestIdx] > array[i]:
                smallestIdx = i
        array[currentIdx], array[smallestIdx] = array[smallestIdx], array[currentIdx]

    return array

15. Tim Sort

import bisect

def timSort(lst):  # in-place | stable
    """
    Python sort(), sorted() implementation
    from https://github.com/hu-ng/timsort/blob/master/timsort.py
    
    Best : O(n) Time | O(n) Space
    Average : O(nlogn) Time | O(n) Space
    Worst : O(nlogn) Time | O(n) Space
    """
    def reverse(lst, s, e):
        """Reverse the order of a list in place
        Input: s = starting index, e = ending index"""
        while s < e and s != e:
            lst[s], lst[e] = lst[e], lst[s]
            s += 1
            e -= 1

    def make_temp_array(lst, s, e):
        """From the lst given, make a copy from index s to index e"""
        array = []
        while s <= e:
            array.append(lst[s])
            s += 1
        return array

    def merge_compute_minrun(n):
        """Returns the minimum length of a run from 23 - 64 so that
        the len(array)/minrun is less than or equal to a power of 2."""
        r = 0
        while n >= 32:
            r |= n & 1
            n >>= 1
        return n + r

    def count_run(lst, s_run):
        """Count the length of one run, returns starting/ending indices,
        a boolean value to present increasing/decreasing run,
        and the length of the run"""
        increasing = True

        # If count_run started at the final position of the array
        if s_run == len(lst) - 1:
            return [s_run, s_run, increasing, 1]
        else:
            e_run = s_run
            # Decreasing run (strictly decreasing):
            if lst[s_run] > lst[s_run + 1]:
                while lst[e_run] > lst[e_run + 1]:
                    e_run += 1
                    if e_run == len(lst) - 1:
                        break
                increasing = False
                return [s_run, e_run, increasing, e_run - s_run + 1]

            # Increasing run (non-decreasing):
            else:
                while lst[e_run] <= lst[e_run + 1]:
                    e_run += 1
                    if e_run == len(lst) - 1:
                        break
                return [s_run, e_run, increasing, e_run - s_run + 1]

    def bin_sort(lst, s, e, extend):
        """Binary insertion sort, assumed that lst[s:e + 1] is sorted.
        Extend the run by the number indicated by 'extend'"""

        for i in range(1, extend + 1):
            pos = 0
            start = s
            end = e + i

            # Value to be inserted
            value = lst[end]

            # If the value is already bigger than the last element from start -> end:
            # Don't do the following steps
            if value >= lst[end - 1]:
                continue

            # While-loop does the binary search
            while start <= end:
                if start == end:
                    if lst[start] > value:
                        pos = start
                        break
                    else:
                        pos = start + 1
                        break
                mid = (start + end) // 2
                if value >= lst[mid]:
                    start = mid + 1
                else:
                    end = mid - 1

            if start > end:
                pos = start

            # 'Push' the elements to the right by 1 element
            # Copy the value back the right position.
            for x in range(e + i, pos, -1):
                lst[x] = lst[x - 1]
            lst[pos] = value

    def gallop(lst, val, low, high, ltr):
        """Find the index of val in the slice[low:high]"""

        if ltr == True:
            # Used for merging from left to right
            # The index found will be so that every element prior
            # to that index is strictly smaller than val
            pos = bisect.bisect_left(lst, val, low, high)
            return pos

        else:
            # Used for merging from right to left
            # The index found will be so that every element from
            # that index onwards is strictly larger than val
            pos = bisect.bisect_right(lst, val, low, high)
            return pos

    def merge(lst, stack, run_num):
        """Merge the two runs and update the remaining runs in the stack
        Only consequent runs are merged, one lower, one upper."""

        # Make references to the to-be-merged runs
        run_a = stack[run_num]
        run_b = stack[run_num + 1]

        # Make a reference to where the new combined run would be.
        new_run = [run_a[0], run_b[1], True, run_b[1] - run_a[0] + 1]

        # Put this new reference in the correct position in the stack
        stack[run_num] = new_run

        # Delete the upper run of the two runs from the stack
        del stack[run_num + 1]

        # If the length of run_a is smaller than or equal to length of run_b
        if run_a[3] <= run_b[3]:
            merge_low(lst, run_a, run_b, 7)

        # If the length of run_a is bigger than length of run_b
        else:
            merge_high(lst, run_a, run_b, 7)

    def merge_low(lst, a, b, min_gallop):
        """Merges the two runs quasi in-place if a is the smaller run
        - a and b are lists that store data of runs
        - min_gallop: threshold needed to switch to galloping mode
        - galloping mode: uses gallop() to 'skip' elements instead of linear merge"""

        # Make a copy of the run a, the smaller run
        temp_array = make_temp_array(lst, a[0], a[1])
        # The first index of the merging area
        k = a[0]
        # Counter for the temp array of a
        i = 0
        # Counter for b, starts at the beginning
        j = b[0]

        gallop_thresh = min_gallop
        while True:
            a_count = 0  # number of times a win in a row
            b_count = 0  # number of times b win in a row

            # Linear merge mode, taking note of how many times a and b wins in a row.
            # If a_count or b_count > threshold, switch to gallop
            while i <= len(temp_array) - 1 and j <= b[1]:

                # if elem in a is smaller, a wins
                if temp_array[i] <= lst[j]:
                    lst[k] = temp_array[i]
                    k += 1
                    i += 1

                    a_count += 1
                    b_count = 0

                    # If a runs out during linear merge
                    # Copy the rest of b
                    if i > len(temp_array) - 1:
                        while j <= b[1]:
                            lst[k] = lst[j]
                            k += 1
                            j += 1
                        return

                    # threshold reached, switch to gallop
                    if a_count >= gallop_thresh:
                        break

                # if elem in b is smaller, b wins
                else:
                    lst[k] = lst[j]
                    k += 1
                    j += 1

                    a_count = 0
                    b_count += 1

                    # If b runs out during linear merge
                    # copy the rest of a
                    if j > b[1]:
                        while i <= len(temp_array) - 1:
                            lst[k] = temp_array[i]
                            k += 1
                            i += 1
                        return

                    # threshold reached, switch to gallop
                    if b_count >= gallop_thresh:
                        break

            # If one run is winning consistently, switch to galloping mode.
            # i, j, and k are incremented accordingly
            while True:
                # Look for the position of b[j] in a
                # bisect_left() -> a_adv = index in the slice [i: len(temp_array)]
                # so that every elem before temp_array[a_adv] is strictly smaller than lst[j]
                a_adv = gallop(temp_array, lst[j], i, len(temp_array), True)

                # Copy the elements prior to a_adv to the merge area, increment k
                for x in range(i, a_adv):
                    lst[k] = temp_array[x]
                    k += 1

                # Update the a_count to check successfulness of galloping
                a_count = a_adv - i

                # Advance i to a_adv
                i = a_adv

                # If run a runs out
                if i > len(temp_array) - 1:
                    # Copy all of b over, if there is any left
                    while j <= b[1]:
                        lst[k] = lst[j]
                        k += 1
                        j += 1
                    return

                # Copy b[j] over
                lst[k] = lst[j]
                k += 1
                j += 1

                # If b runs out
                if j > b[1]:
                    # Copy all of a over, if there is any left
                    while i < len(temp_array):
                        lst[k] = temp_array[i]
                        k += 1
                        i += 1
                    return

                # ------------------------------------------------------

                # Look for the position of a[i] in b
                # b_adv is analogous to a_adv
                b_adv = gallop(lst, temp_array[i], j, b[1] + 1, True)
                for y in range(j, b_adv):
                    lst[k] = lst[y]
                    k += 1

                # Update the counters and check the conditions
                b_count = b_adv - j
                j = b_adv

                # If b runs out
                if j > b[1]:
                    # copy the rest of a over
                    while i <= len(temp_array) - 1:
                        lst[k] = temp_array[i]
                        k += 1
                        i += 1
                    return

                # copy a[i] over to the merge area
                lst[k] = temp_array[i]
                i += 1
                k += 1

                # If a runs out
                if i > len(temp_array) - 1:
                    # copy the rest of b over
                    while j <= b[1]:
                        lst[k] = lst[j]
                        k += 1
                        j += 1
                    return

                # if galloping proves to be unsuccessful, return to linear
                if a_count < gallop_thresh and b_count < gallop_thresh:
                    break

            # punishment for leaving galloping
            # makes it harder to enter galloping next time
            gallop_thresh += 1

    def merge_high(lst, a, b, min_gallop):
        """Merges the two runs quasi in-place if b is the smaller run
        - Analogous to merge_low, but starts from the end
        - a and b are lists that store data of runs
        - min_gallop: threshold needed to switch to galloping mode
        - galloping mode: uses gallop() to 'skip' elements instead of linear merge"""

        # Make a copy of b, the smaller run
        temp_array = make_temp_array(lst, b[0], b[1])

        # Counter for the merge area, starts at the last index of array b
        k = b[1]
        # Counter for the temp array

        i = len(temp_array) - 1  # Lower bound is 0

        # Counter for a, starts at the end this time
        j = a[1]

        gallop_thresh = min_gallop
        while True:
            a_count = 0  # number of times a win in a row
            b_count = 0  # number of times b win in a row

            # Linear merge, taking note of how many times a and b wins in a row.
            # If a_count or b_count > threshold, switch to gallop
            while i >= 0 and j >= a[0]:
                if temp_array[i] > lst[j]:
                    lst[k] = temp_array[i]
                    k -= 1
                    i -= 1

                    a_count = 0
                    b_count += 1

                    # If b runs out during linear merge
                    if i < 0:
                        while j >= a[0]:
                            lst[k] = lst[j]
                            k -= 1
                            j -= 1
                        return

                    if b_count >= gallop_thresh:
                        break

                else:
                    lst[k] = lst[j]
                    k -= 1
                    j -= 1

                    a_count += 1
                    b_count = 0

                    # If a runs out during linear merge
                    if j < a[0]:
                        while i >= 0:
                            lst[k] = temp_array[i]
                            k -= 1
                            i -= 1
                        return

                    if a_count >= gallop_thresh:
                        break

            # i, j, k are DECREMENTED in this case
            while True:
                # Look for the position of b[i] in a[0, j + 1]
                # ltr = False -> uses bisect_right()
                a_adv = gallop(lst, temp_array[i], a[0], j + 1, False)

                # Copy the elements from a_adv -> j to merge area
                # Go backwards to the index a_adv
                for x in range(j, a_adv - 1, -1):
                    lst[k] = lst[x]
                    k -= 1

                # # Update the a_count to check successfulness of galloping
                a_count = j - a_adv + 1

                # Decrement index j
                j = a_adv - 1

                # If run a runs out:
                if j < a[0]:
                    while i >= 0:
                        lst[k] = temp_array[i]
                        k -= 1
                        i -= 1
                    return

                # Copy the b[i] into the merge area
                lst[k] = temp_array[i]
                k -= 1
                i -= 1

                # If a runs out:
                if i < 0:
                    while j >= a[0]:
                        lst[k] = lst[j]
                        k -= 1
                        j -= 1
                    return

                # -------------------------------------------------

                # Look for the position of A[j] in B:
                b_adv = gallop(temp_array, lst[j], 0, i + 1, False)
                for y in range(i, b_adv - 1, -1):
                    lst[k] = temp_array[y]
                    k -= 1

                b_count = i - b_adv + 1
                i = b_adv - 1

                # If b runs out:
                if i < 0:
                    while j >= a[0]:
                        lst[k] = lst[j]
                        k -= 1
                        j -= 1
                    return

                # Copy the a[j] back to the merge area
                lst[k] = lst[j]
                k -= 1
                j -= 1

                # If a runs out:
                if j < a[0]:
                    while i >= 0:
                        lst[k] = temp_array[i]
                        k -= 1
                        i -= 1
                    return

                # if galloping proves to be unsuccessful, return to linear
                if a_count < gallop_thresh and b_count < gallop_thresh:
                    break

            # punishment for leaving galloping
            gallop_thresh += 1

    def merge_collapse(lst, stack):
        """The last three runs in the stack is A, B, C.
        Maintains invariants so that their lengths: A > B + C, B > C
        Translated to stack positions:
        stack[-3] > stack[-2] + stack[-1]
        stack[-2] > stack[-1]
        Takes a stack that holds many lists of type [s, e, bool, length]"""

        # This loops keeps running until stack has one element
        # or the invariant holds.
        while len(stack) > 1:
            if len(stack) >= 3 and stack[-3][3] <= stack[-2][3] + stack[-1][3]:
                if stack[-3][3] < stack[-1][3]:
                    # merge -3 and -2, merge at -3
                    merge(lst, stack, -3)
                else:
                    # merge -2 and -1, merge at -2
                    merge(lst, stack, -2)
            elif stack[-2][3] <= stack[-1][3]:
                # merge -2 and -1, merge at -2
                merge(lst, stack, -2)
            else:
                break

    def merge_force_collapse(lst, stack):
        """When the invariant holds and there are > 1 run
        in the stack, this function finishes the merging"""
        while len(stack) > 1:
            # Only merges at -2, because when the invariant holds,
            # merging would be balanced
            merge(lst, stack, -2)

    # Starting index
    s = 0

    # Ending index
    e = len(lst) - 1

    # The stack
    stack = []

    # Compute min_run using size of lst
    min_run = merge_compute_minrun(len(lst))

    while s <= e:

        # Find a run, return [start, end, bool, length]
        run = count_run(lst, s)

        # If decreasing, reverse
        if run[2] == False:
            reverse(lst, run[0], run[1])
            # Change bool to True
            run[2] = True

        # If length of the run is less than min_run
        if run[3] < min_run:
            # The number of indices by which we want to extend the run
            # either by the distance to the end of the lst
            # or by the length difference between run and minrun
            extend = min(min_run - run[3], e - run[1])

            # Extend the run using binary insertion sort
            bin_sort(lst, run[0], run[1], extend)

            # Update last index of the run
            run[1] = run[1] + extend

            # Update the run length
            run[3] = run[3] + extend

        # Push the run into the stack
        stack.append(run)

        # Start merging to maintain the invariant
        merge_collapse(lst, stack)

        # Update starting position to find the next run
        # If run[1] == end of the lst, s > e, loop exits
        s = run[1] + 1

    # Some runs might be left in the stack, complete the merging.
    merge_force_collapse(lst, stack)

    return lst

 

속도 테스트

1. 크기 100

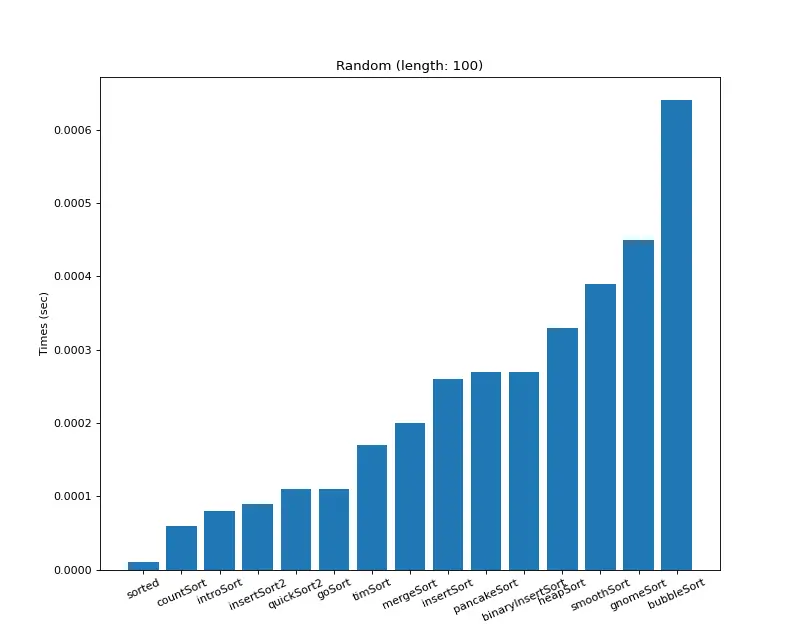
 크기 100 (랜덤)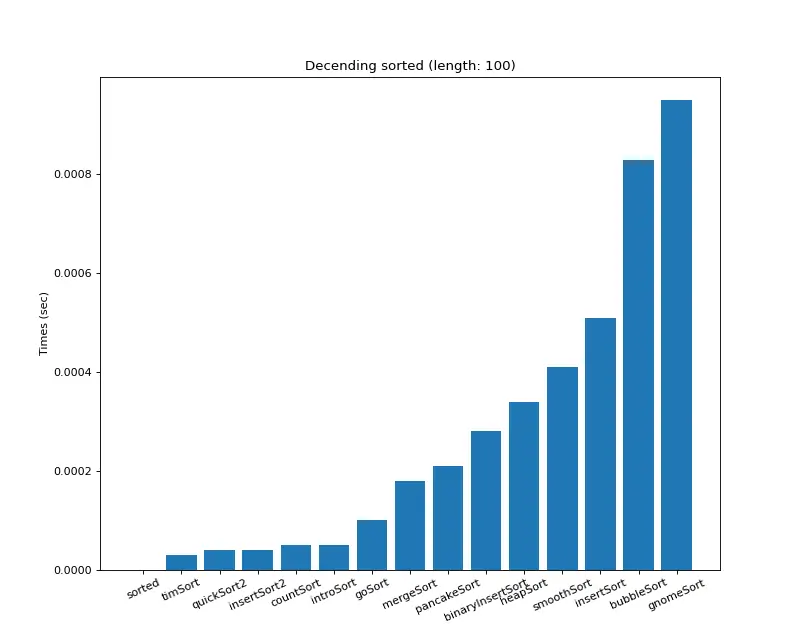

크기 100 (내림차순 배열)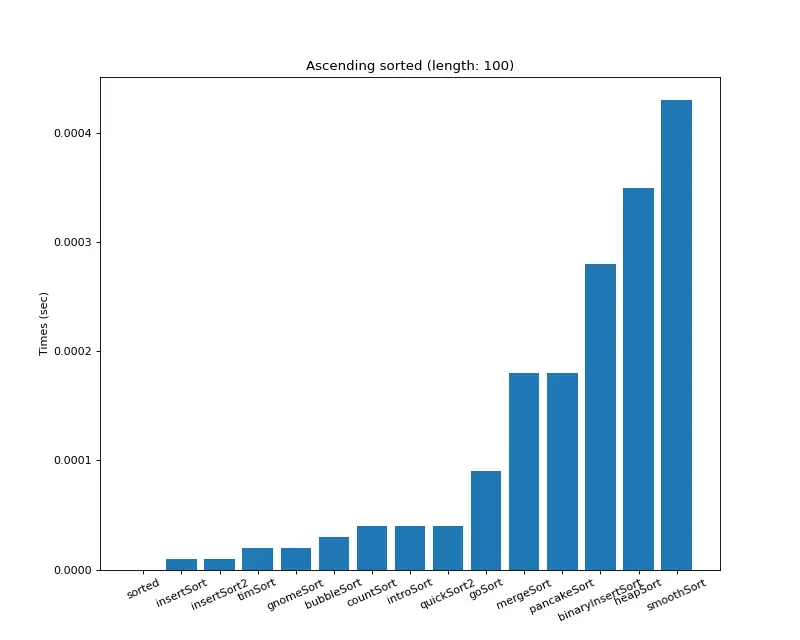

크기 100 (오름차순 배열)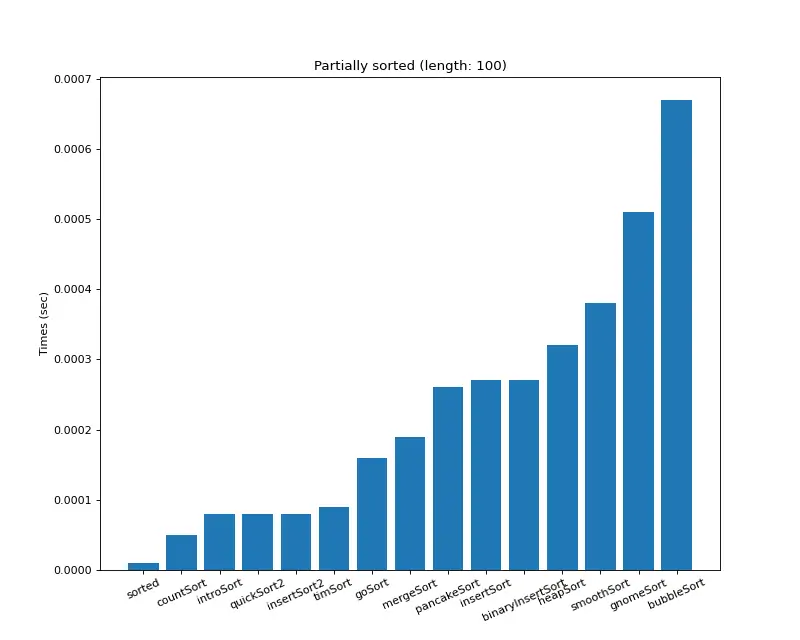

크기 100 (부분 정렬)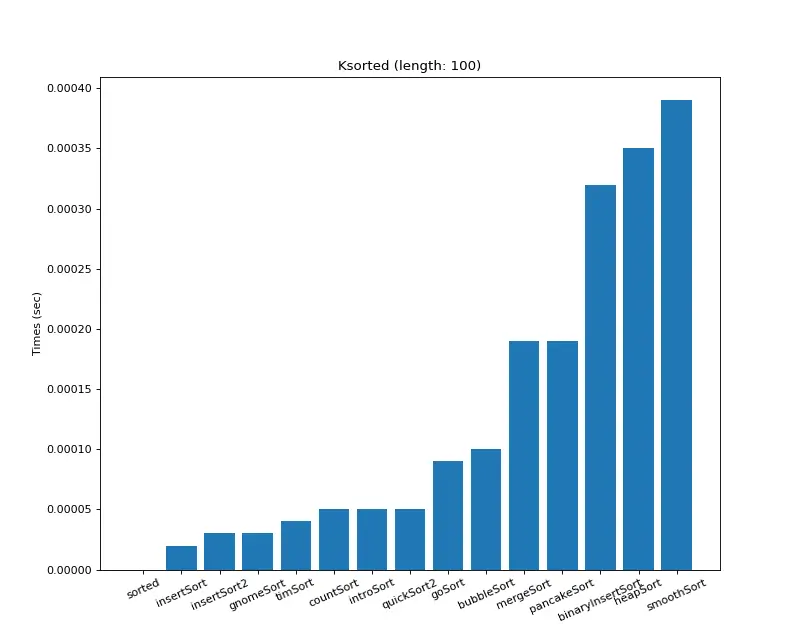

크기 100 (K정렬)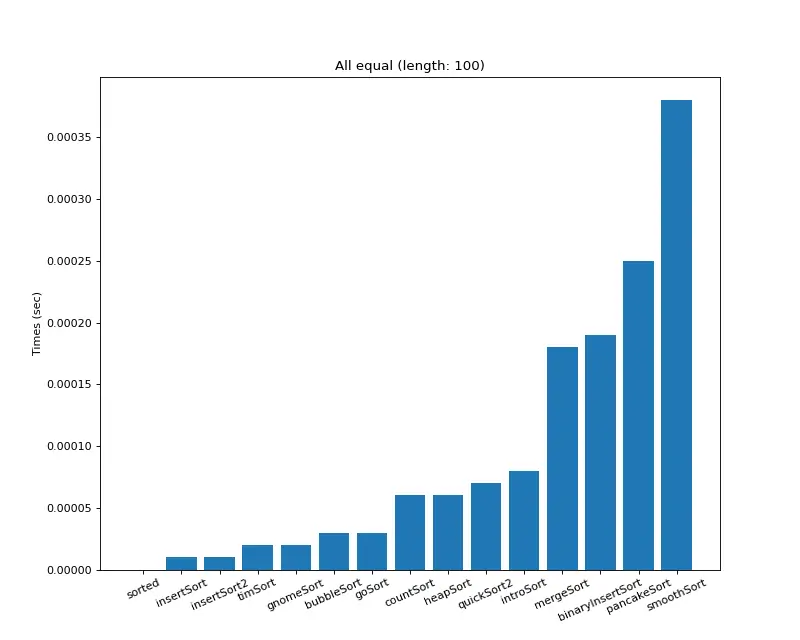

크기 100 (모두 같은 값)

크기 100 (거의 모두 같은 값)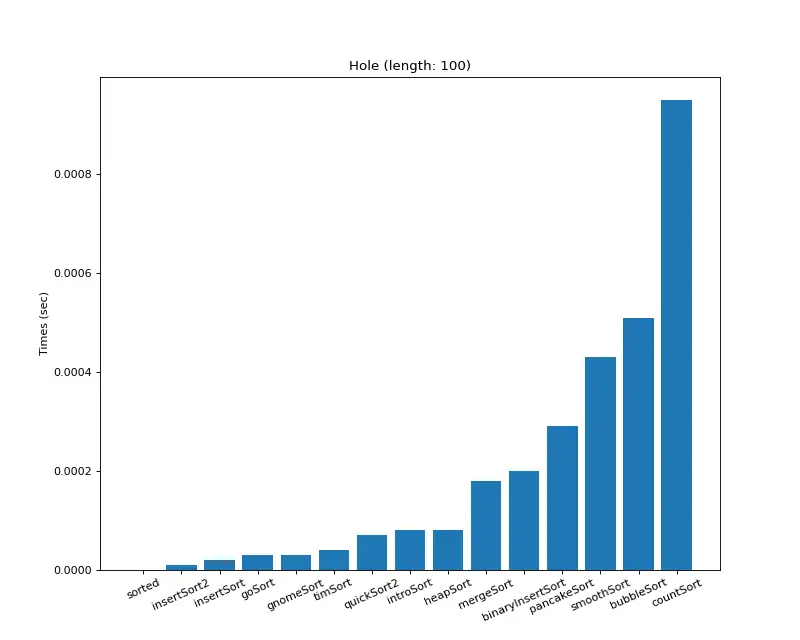

크기 100 (하나만 다른 값)

 

2. 크기 10,000

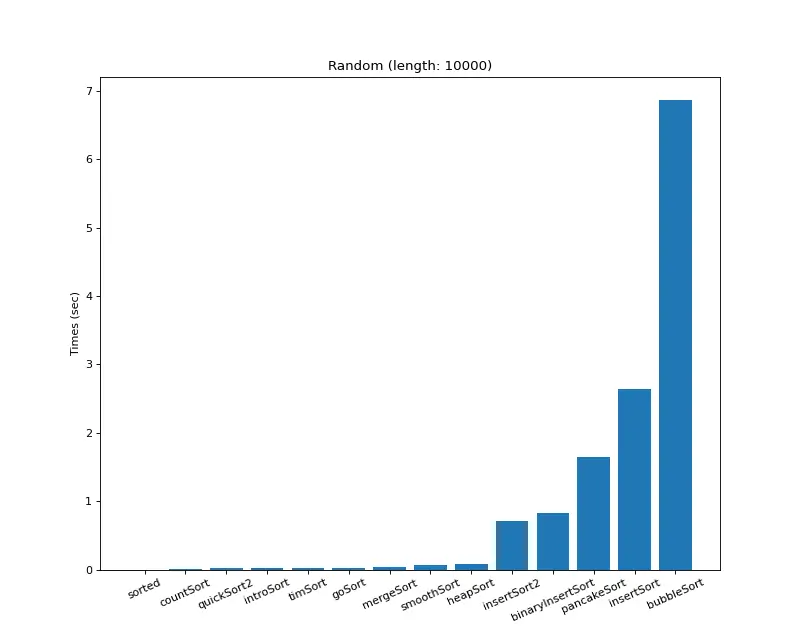
크기 10,000 (랜덤)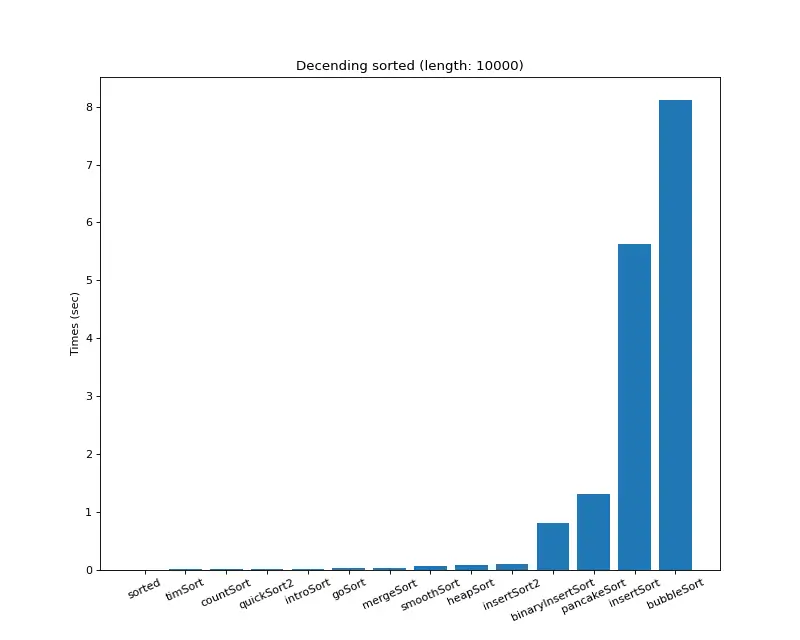

크기 10,000 (내림차순 배열)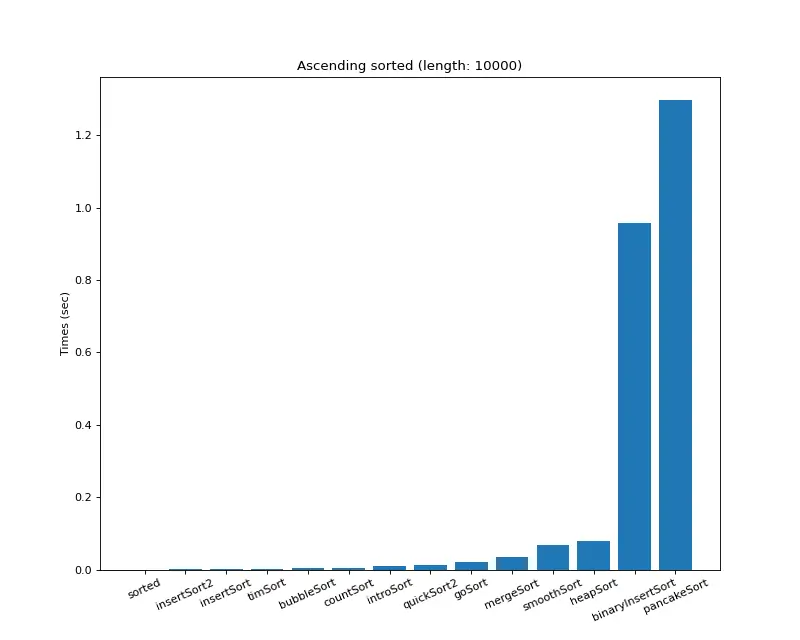

크기 10,000 (오름차순 배열)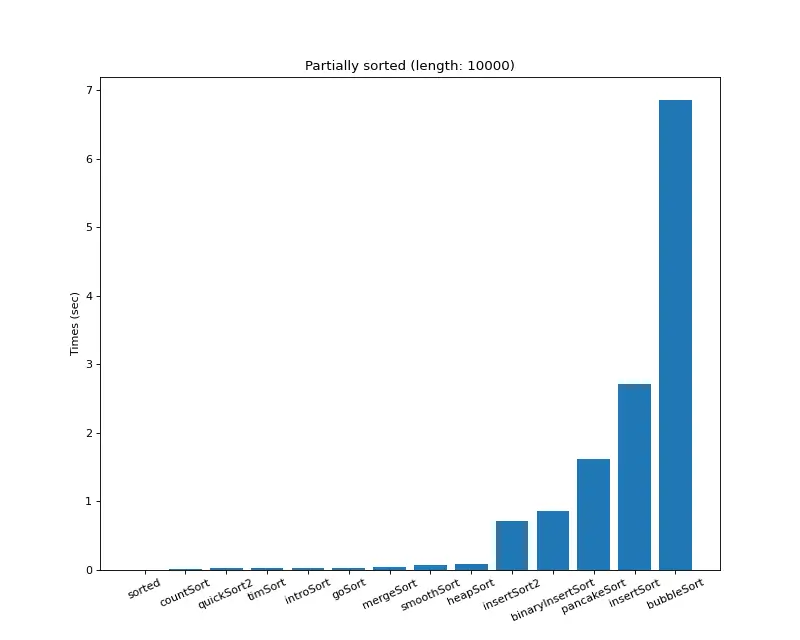

크기 10,000 (부분 정렬)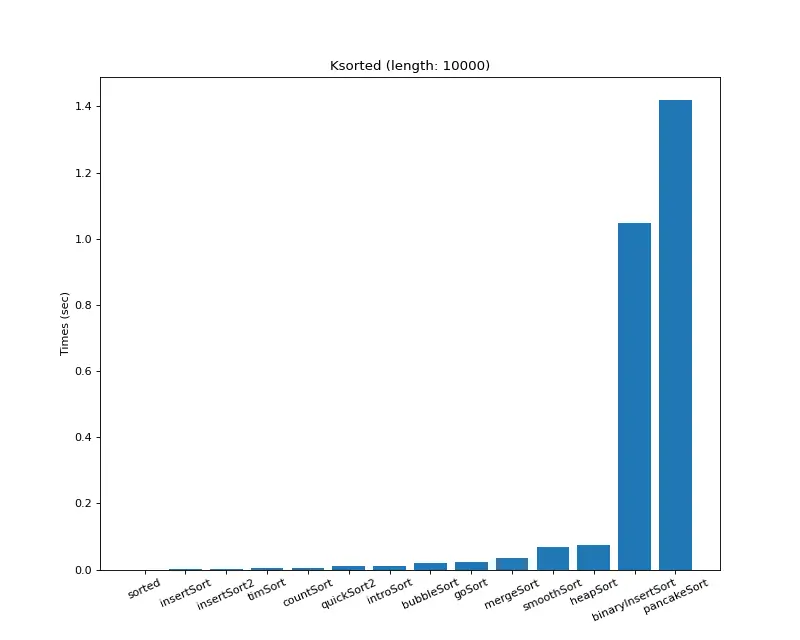

크기 10,000 (K정렬)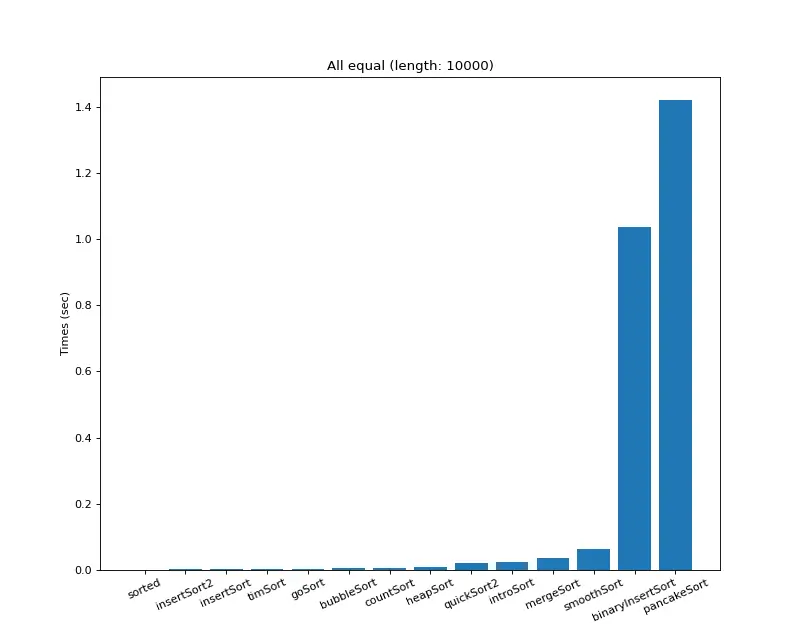

크기 10,000 (모두 같은 값)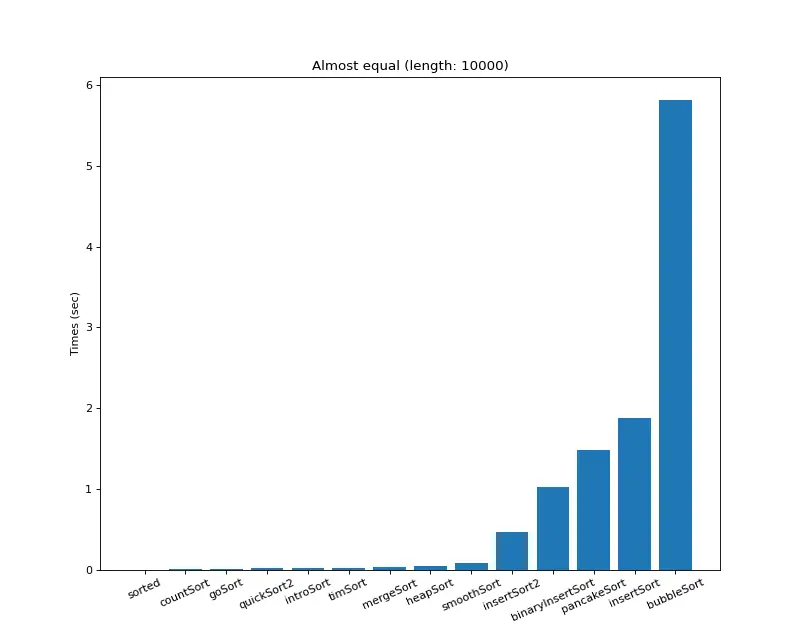

크기 10,000 (거의 모두 같은 값)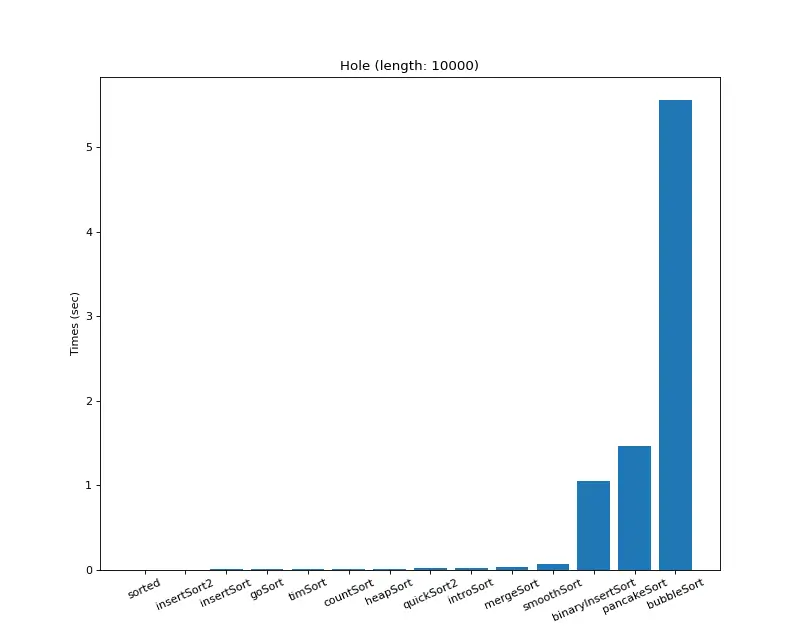

크기 10,000 (하나만 다른 값)

 

3. 크기 1,000,000 (백만)

크기 백만 (랜덤)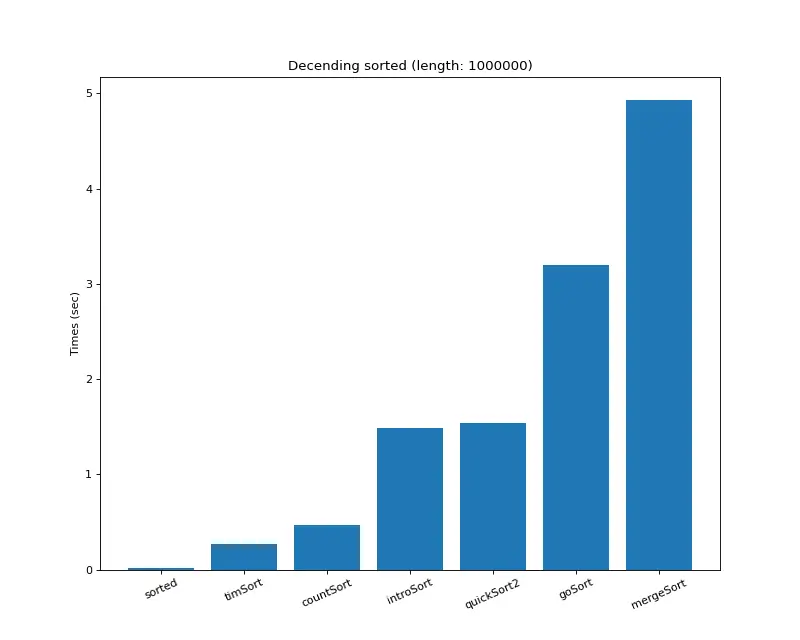

크기 백만 (내림차순 배열)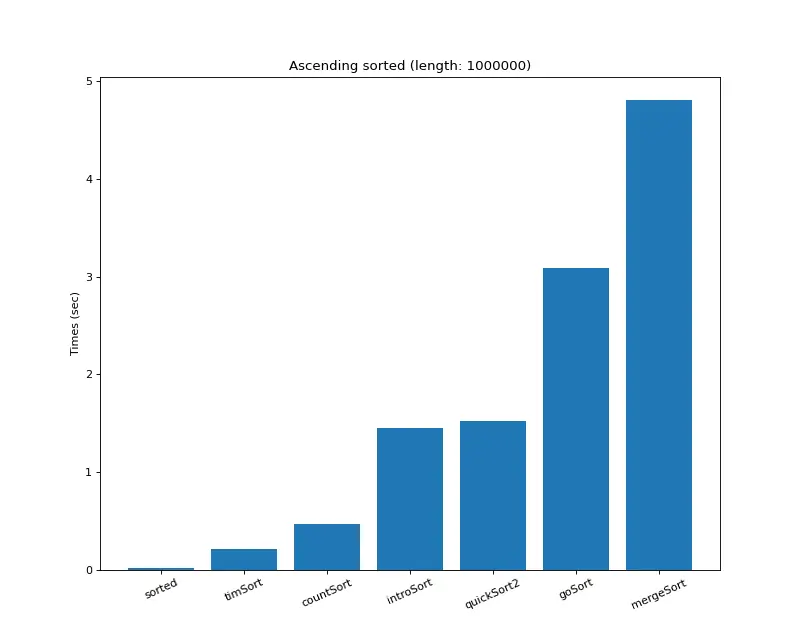

크기 백만 (오름차순 배열)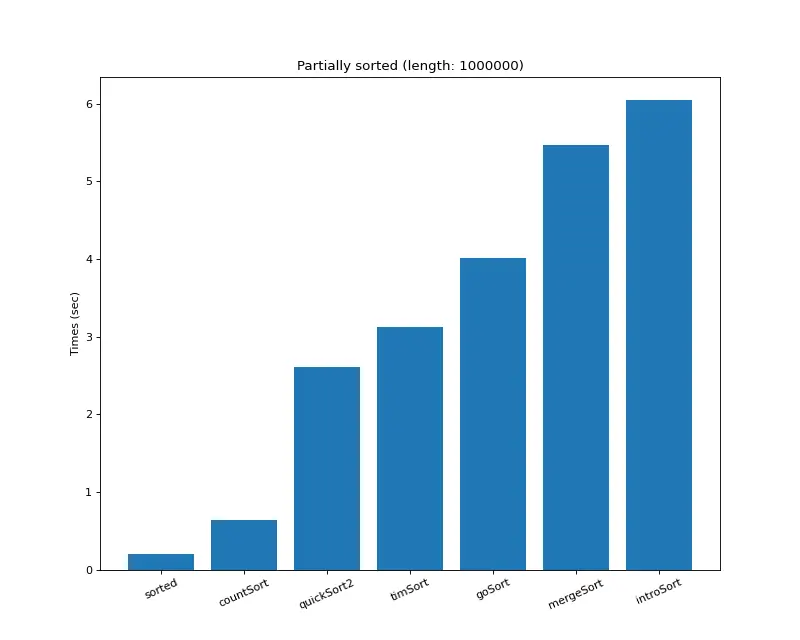

크기 백만 (부분 정렬)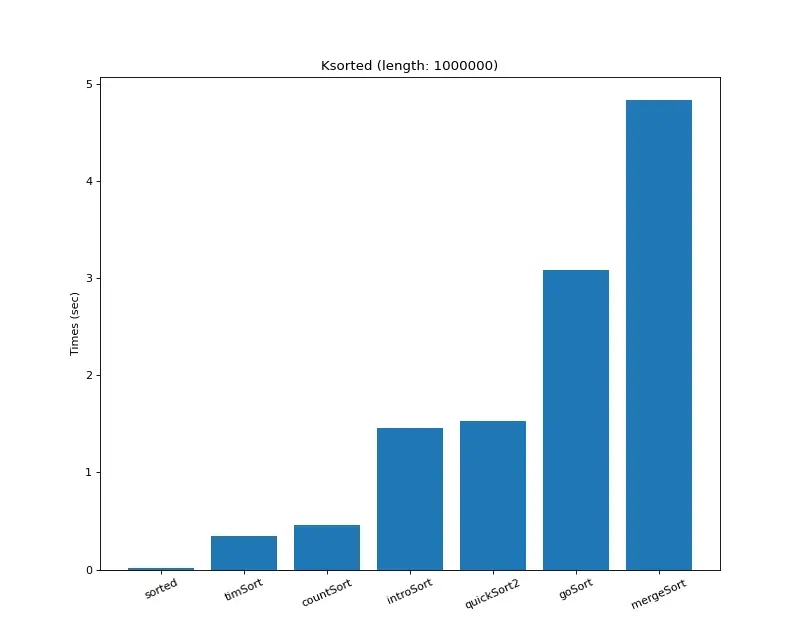

크기 백만 (k정렬)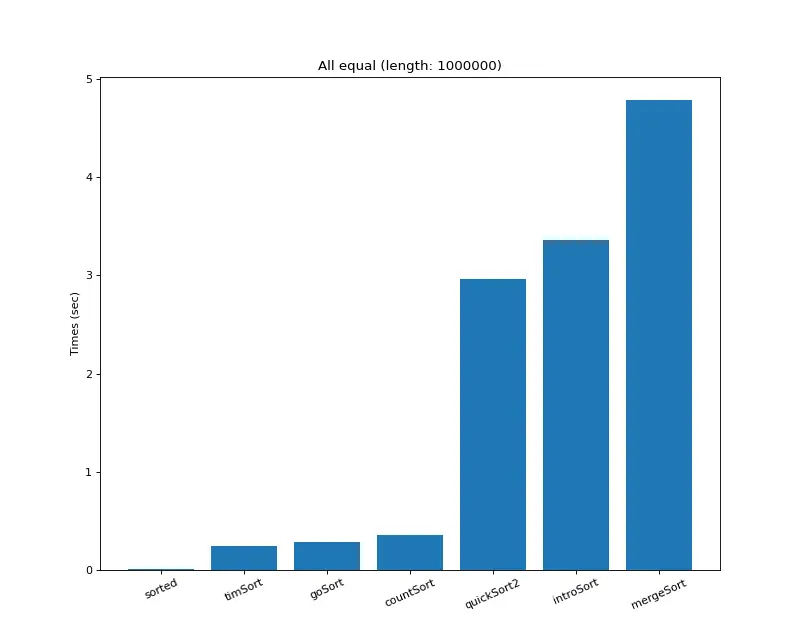

크기 백만 (다 같은 값)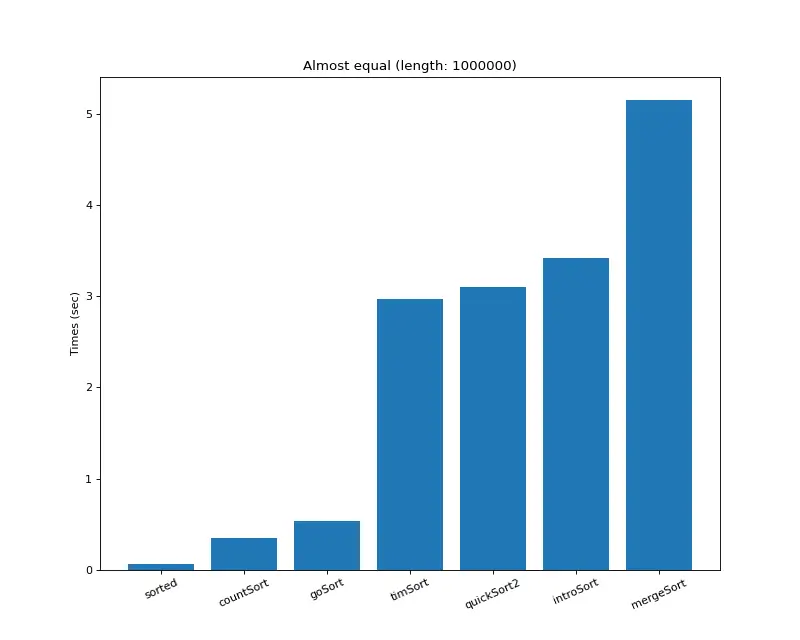

크기 백만 (거의 모두 같은 값)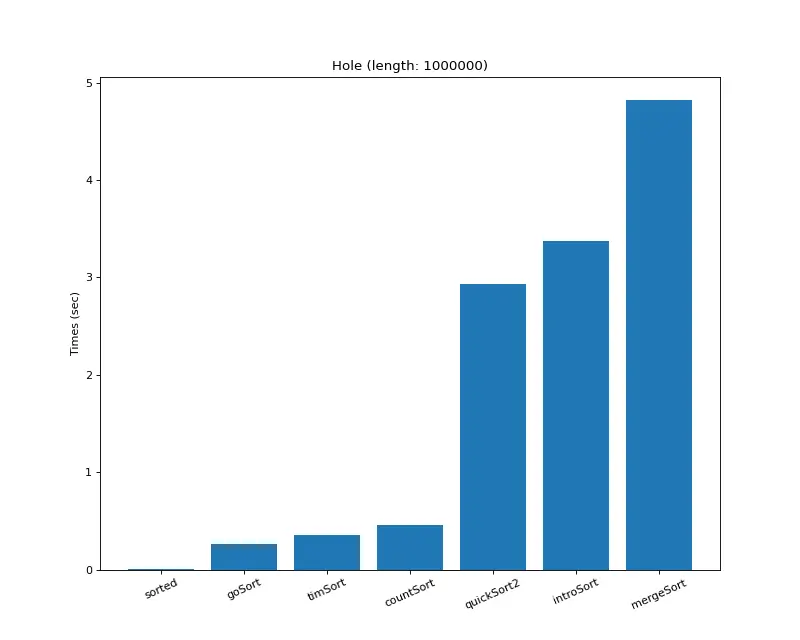

크기 백만 (하나만 다른 값)

 

배열 생성기 및 시간 복잡도 계산기 : choiseokwon.tistory.com/231

파이썬 정렬 알고리즘 big-O 시간 복잡도 계산하기

풀 코드 확인하기 : https://gist.github.com/Alfex4936/e8b6b7c06a181d3faa84b155b20e6de6

TimSort + Introspective Sort + bogo Sort + pancake Sort + Insertion Sort + Binary Insertion Sort + Count Sort + Merge Sort + Qui

※ 부정확한 코드들도 있음