파이썬 Smooth Sort (부드러운 정렬 알고리즘)

Smooth Sort

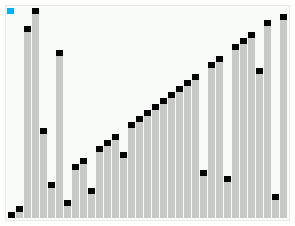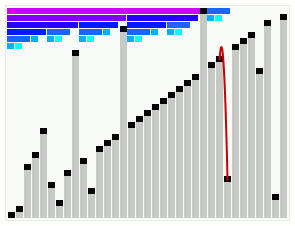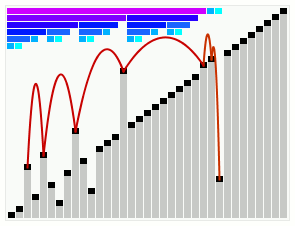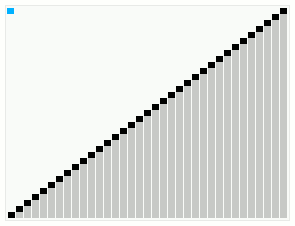
@wikipedia

소개 : 부드러운 정렬은 길 찾기로 유명한 데이크스트라분이 1981년에 발표한 정렬 알고리즘이다.

HeapSort의 변형 중 하나이며, in-place, not stable

시간 복잡도는 최고 : O($n$) = (대부분 정렬된 상태일 경우)

평균 : O($nlogn$), 최악 : O($nlogn$) 공간 복잡도는 총 O($n$), 보조(O($1$))

특이한 점은 Leonardo number라는 수학 개념을 Heap Sort에 적용시킨 점이다.

 

1. Leonardo Number

피보나치 수열과 비슷한데, 다음과 같이 진행된다.

$1, 1, 3, 5, 9, 15, 25, 41, 67, 109, 177, 287, 465, 753, 1219, 1973, 3193, 5167, 8361 ...$

실제로 아래 수식을 적용하면 피보나치 수열로 바꿀 수 있다.

$L(n) = 2F(n + 1) - 1, n >= 0$

 

그럼 이 Leonardo Number를 어떻게 정렬 알고리즘에 사용했을까? 일단 파이썬 코드를 보겠다.

def numbersLeonardo(size):
    numbers = [1, 1]
    nextNumber = numbers[-1] + numbers[-2] + 1
    while len(numbers) >= 2 and size > nextNumber:
        numbers.append(nextNumber)
        nextNumber = numbers[-1] + numbers[-2] + 1
    numbers.reverse()
    return numbers
    
    
def arrToHeap(data):  # 배열을 받으면 heap 구조로 바꿈
    leonardoNumbers = numbersLeonardo(len(data))
    listHeaps = []
    m = 0
 
    for i in leonardoNumbers:
        # 아직 할당 안된 배열이 다음 레오나르도 수보다 크거나 같으면
        if len(data) - m >= i:
            listHeaps.append(data[m: m+i])
            # 할당 안된 부분으로 이동
            m += i
    # 힙 성질 맞추기
    for i in listHeaps:
        heapq.heapify(i)
    # heap은 non-decreasing이기 때문에 뒤집기
    listHeaps.reverse()
    return listHeaps

자식 노드는 절대 부모보다 큰 값을 가질 수 없고 (둘 다 1일 땐 예외)

자식들의 크기는 레오나르도 수열을 따라서, 힙은 아래처럼 생성된다.

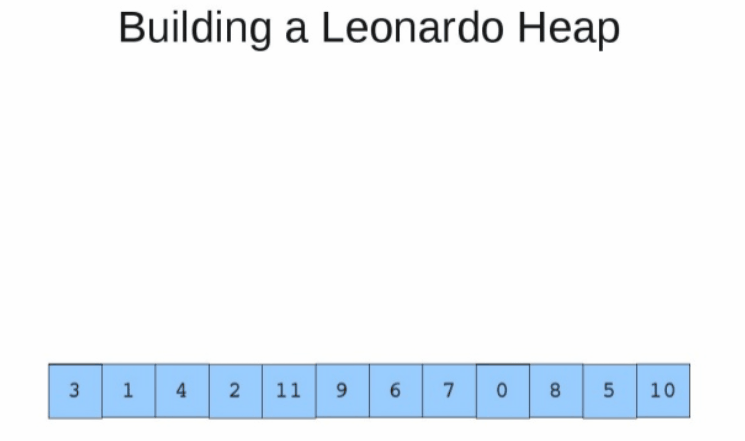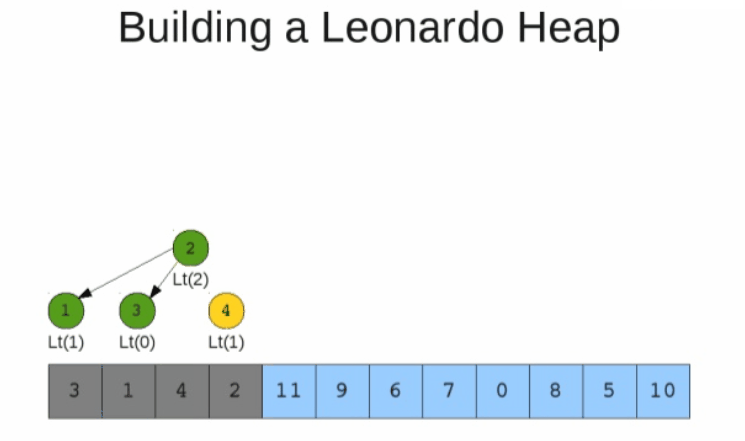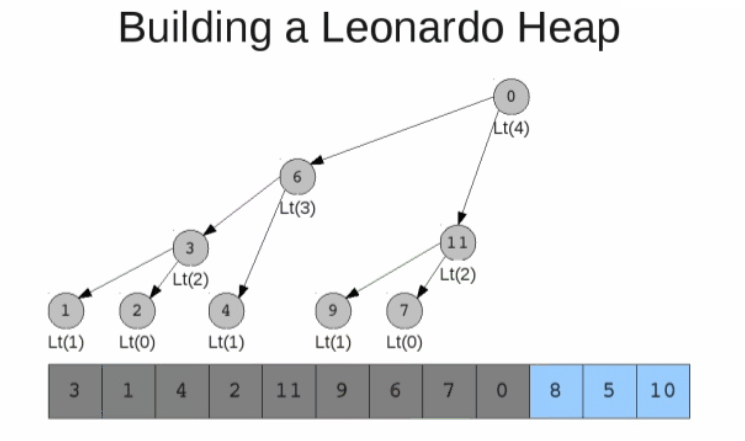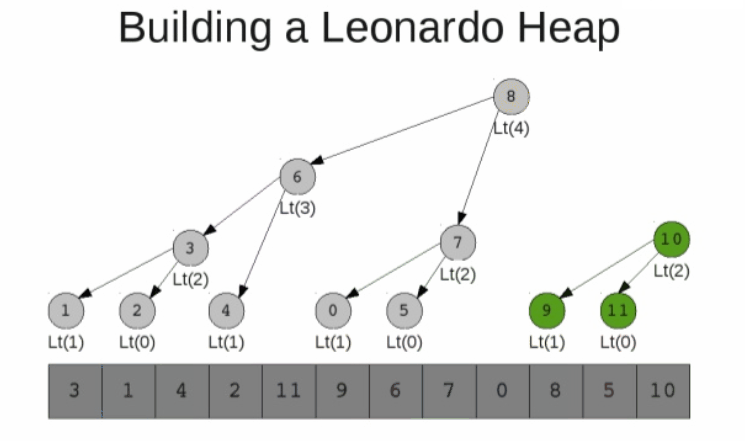
Dijikstra : 누군가는 제가  왜 stretch 길이에 레오나르도 수를 사용했는지 물을 수 있습니다,

... 63 31 15 7 3 1, 이 수들은 곧 확률이고,

Completely Balanced 트리에서 각 stretch는 후위 순회(post-order) 결과처럼 보였습니다.

저는 제가 왜 레오나르도 수를 선택했는지 잘 알고 있습니다, Balanced 트리에서 stretch 평균 수는 레오나르도 수들에

$1.2559$ ( = $(1/4) · (5+sqrt(5)) · (log2(1+sqrt(5))-1$) 배를 한 것과 같았기 때문이죠.

음...말이 어렵다

stretch = 각 노드를 이 노드보다 값이 작은 K 개의 노드들로 바꾸는 것

ex) 아래 트리에 stretch(3)을 하면, root(12)는 값 4의 노드 3개를 갖고, node(81)은 값 34의 노드 3개로 stretch

root = Node(12)
root.left = Node(81)
root.left.right = Node(56)

 

2. Smooth Sort 구현하기

사실 Leonardo 수를 이용한 것 빼고는 별 것 없다.

Heap Sort에 Leonardo 수를 이용해 heap만 만들면 되기 때문이다.

(Heaps들이 완전한 Balanced 상태는 아니다, 그래서 remark3, 힙 크기를 N^2 - 1로 하면 balanced가 됨)

import heapq


def numbersLeonardo(size):
    numbers = [1, 1]
    nextNumber = numbers[-1] + numbers[-2] + 1
    while len(numbers) >= 2 and size > nextNumber:
        numbers.append(nextNumber)
        nextNumber = numbers[-1] + numbers[-2] + 1
    numbers.reverse()
    return numbers
    
    
def arrToHeap(data):  # 배열을 받으면 heap 구조로 바꿈
    leonardoNumbers = numbersLeonardo(len(data))
    listHeaps = []
    m = 0
    for i in leonardoNumbers:
        # 아직 할당 안된 배열이 다음 레오나르도 수보다 크거나 같으면
        if len(data) - m >= i:
            listHeaps.append(data[m: m+i])
            # 할당 안된 부분으로 이동
            m += i
    # 힙 성질 맞추기
    for i in listHeaps:
        heapq.heapify(i)
    # heap은 non-decreasing이기 때문에 뒤집기
    listHeaps.reverse()
    return listHeaps


def countIndexes(i, indexes):
    indexes.append(2*indexes[i]+1)
    indexes.append(2*indexes[i]+2)

    return indexes


def getList(indexPart, heap):
    heapPart = []
    for i in indexPart:
        if i < len(heap):
            heapPart.append(heap[i])

    return heapPart


def heapDivision(heap):
    heapleft = []
    heapright = []
    index = 0
    indexesLeft = [1]
    indexesRight = [2]
    while indexesLeft[-1] < len(heap):

        indexesLeft = countIndexes(index, indexesLeft)

        indexesRight = countIndexes(index, indexesRight)

        index += 1

    heapleft = getList(indexesLeft, heap)
    heapright = getList(indexesRight, heap)

    return heapleft, heapright

# Time Complexity O(n) | O(nlogn) | O(nlogn)
# Space Complexity AUX : O(1), Total : O(n)
def smoothSort(array):
    listHeaps = arrToHeap(array)
    result = []
    heapLeft, heapRight = 0, 0

    while (listHeaps):
        flag = 0
        minIndex = listHeaps.index(min(listHeaps))
        currentRoot = listHeaps[0][0]
        currentMin = listHeaps[minIndex][0]
        heapq.heapreplace(listHeaps[0], currentMin)
        heapq.heapreplace(listHeaps[minIndex], currentRoot)
        if len(listHeaps[0]) > 1:
            heapLeft, heapRight = heapDivision(listHeaps[0])
            flag = 1
        minimum = heapq.heappop(listHeaps[0])
        result.append(minimum)
        listHeaps.pop(0)
        if flag == 1:
            listHeaps.insert(0, heapLeft)
            listHeaps.insert(0, heapRight)
    return result

 

3. 얼마나 빠른가?

테스트 배열을 3번 실행해서, 가장 빠르게 정렬된 시간을 출력하도록 했다.

1. 랜덤한 숫자 5000개

array = [randint(-5000, 5000) for i in range(5000)]

# 결과
def: sorted(), 최소 실행 시간: 0.00100초
def: countSort(), 최소 실행 시간: 0.00300초
def: introSort(), 최소 실행 시간: 0.01400초
def: quickSort(), 최소 실행 시간: 0.01800초
def: mergeSort(), 최소 실행 시간: 0.02400초
def: smoothSort(), 최소 실행 시간: 0.03200초
def: timSort(), 최소 실행 시간: 0.03500초
def: heapSort(), 최소 실행 시간: 0.03500초
def: insertSort(), 최소 실행 시간: 1.59100초
def: bubbleSort(), 최소 실행 시간: 2.55200초

1위 : arr.sorted(), 2위 : countSort(), 3위 : introSort()

4위 : quickSort(), 5위: mergeSort(), 6위: smoothSort()

7위 : timSort(), 8위: heapSort(), 9위 : insertSort(), 10위: bubbleSort()

 

2. 거꾸로 정렬된 크기 5000의 배열 (Descending)

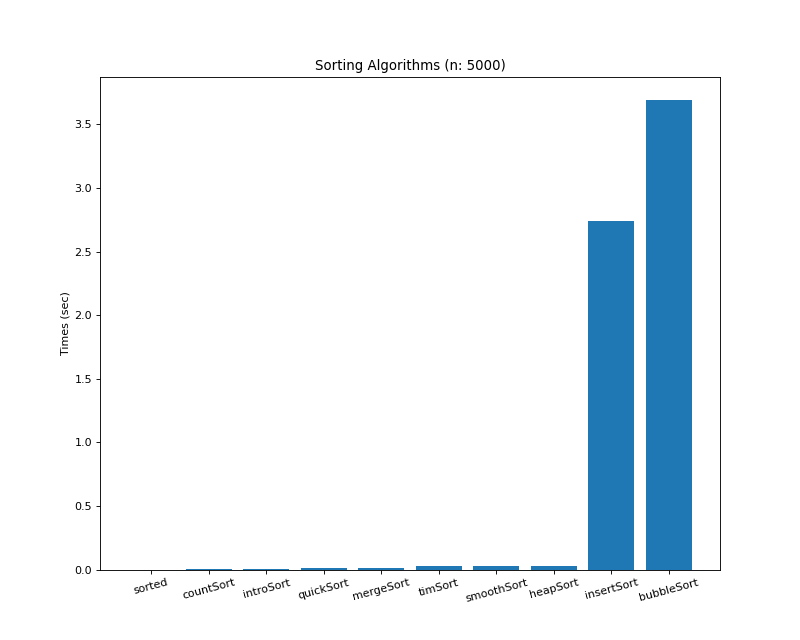
array = [i for i in reversed(range(5000))]

# 결과
def: sorted(), 최소 실행 시간: 0.00000초
def: countSort(), 최소 실행 시간: 0.00200초
def: introSort(), 최소 실행 시간: 0.00600초
def: quickSort(), 최소 실행 시간: 0.01400초
def: mergeSort(), 최소 실행 시간: 0.01500초
def: timSort(), 최소 실행 시간: 0.02600초
def: smoothSort(), 최소 실행 시간: 0.02800초
def: heapSort(), 최소 실행 시간: 0.02900초
def: insertSort(), 최소 실행 시간: 2.73700초
def: bubbleSort(), 최소 실행 시간: 3.69000초

1위 : arr.sorted(), 2위 : countSort(), 3위 : introSort()

4위 : quickSort(), 5위: mergeSort(), 6위: timSort()

7위 : smoothSort(), 8위: heapSort(), 9위 : insertSort(), 10위: bubbleSort()

 

3. 정렬된 크기 5000 배열 (Ascending)

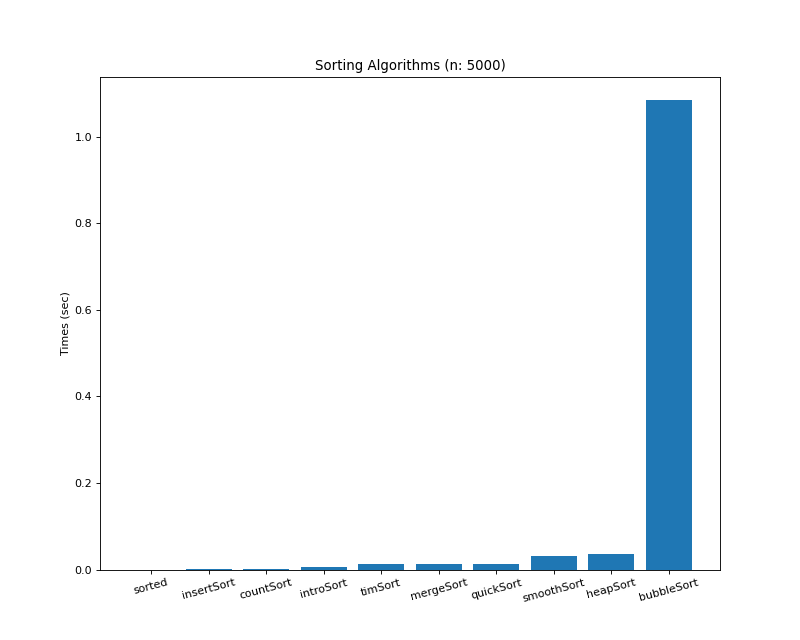
array = [i for i in range(5000)]

# 결과
def: sorted(), 최소 실행 시간: 0.00000초
def: insertSort(), 최소 실행 시간: 0.00100초
def: countSort(), 최소 실행 시간: 0.00200초
def: introSort(), 최소 실행 시간: 0.00600초
def: timSort(), 최소 실행 시간: 0.01300초
def: mergeSort(), 최소 실행 시간: 0.01300초
def: quickSort(), 최소 실행 시간: 0.01400초
def: smoothSort(), 최소 실행 시간: 0.03100초
def: heapSort(), 최소 실행 시간: 0.03600초
def: bubbleSort(), 최소 실행 시간: 1.08400초

1위 : arr.sorted(), 2위 : insertSort(), 3위 : countSort()

4위 : introSort(), 5위: timSort(), 6위: mergeSort()

7위 : quickSort(), 8위: smoothSort(), 9위 : heapSort(), 10위: bubbleSort()

 

4. 크기 5000의 부분 정렬된 랜덤 배열

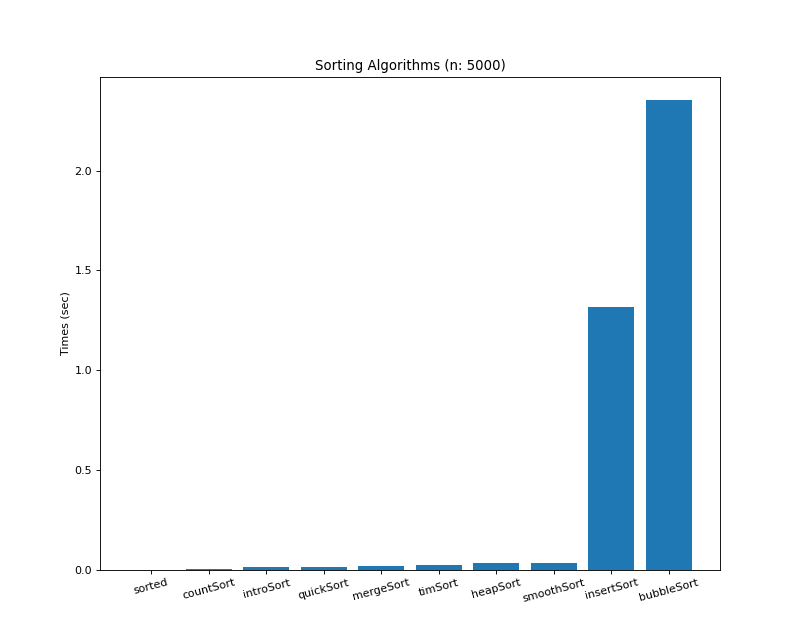
array4 = [randint(-5000, 5000)
              for i in range(5000//3)] + \
        [i for i in range(5000//3)] + \
        [1] + \
        [i for i in reversed(range(5000//3))]

# 결과
def: sorted(), 최소 실행 시간: 0.00000초
def: countSort(), 최소 실행 시간: 0.00300초
def: introSort(), 최소 실행 시간: 0.01200초
def: quickSort(), 최소 실행 시간: 0.01300초
def: mergeSort(), 최소 실행 시간: 0.01800초
def: timSort(), 최소 실행 시간: 0.02100초
def: heapSort(), 최소 실행 시간: 0.03100초
def: smoothSort(), 최소 실행 시간: 0.03100초
def: insertSort(), 최소 실행 시간: 1.31700초
def: bubbleSort(), 최소 실행 시간: 2.35200초

1위 : arr.sorted(), 2위 : countSort(), 3위 : introSort()

4위 : quickSort(), 5위: mergeSort(), 6위: timSort()

7위 : heapSort(), 8위: smoothSort(), 9위 : insertSort(), 10위: bubbleSort()

 

참고 : https://github.com/jasondavies/smoothsort.js/blob/master/smoothsort.js

참고 : https://code.google.com/archive/p/combsortcs2p-and-other-sorting-algorithms/wikis/SmoothSort.wiki

참고 : http://www.cs.utexas.edu/users/EWD/transcriptions/EWD07xx/EWD796a.html