파이썬 Introspective Sort (내성 정렬) 알고리즘

Introspective Sort

@VirtuosicAI

IntroSort (Introspective Sort) 인트로 정렬은, Quick Sort의 장점을 유지하면서,

최악 시나리오 O(n^2)를 해결하려 만들어진 (Quick Sort + Heap Sort + Insertion Sort) 하이브리드 알고리즘이다.

(C++ 기본 정렬 알고리즘, std::sort)

 

모든 상황에서 시간 복잡도 : O(nlogn), 공간 복잡도는 O(logn)이며, inplace, not stable한 알고리즘이다.

(in-place란, 보조 데이터 구조를 사용하지 않고, 작동하는 알고리즘)

 

 Quick Sort로 시작해서, Recursion max-depth (log(len(array)) 에 도달하면 Heap Sort로 정렬하고,

그리고, 파티션 크기가 보통 16보다 작으면 Insertion Sort로 정렬한다.

 

Pseudo Code

 # Intro Sort 주요 특징
 /*
 1. 3개의 요소들에게서 중간값(median) 구하기
 2. 크기가 작은 (보통 16) 파티션들은 Insertion Sort
 3. Quick Sort 하다가 max recursion depth 도달하면 Heap Sort
 */
 
procedure sort(A : array):
    let maxdepth = ⌊log(length(A))⌋ × 2
    introsort(A, maxdepth)

procedure introsort(A, maxdepth):
    n ← length(A)
    size ← endIdx - startIdx
    if n ≤ 1:
        return  // base case
    else if maxdepth = 0:
        heapsort(A)
    else if size < 16:
        insertsort(A)
    else:
    	// pivot, p
        p ← partition(A)  
        introsort(A[0:p-1], maxdepth - 1)
        introsort(A[p+1:n], maxdepth - 1)
        

0. Insertion Sort 구현

Insertion Sort Visualization

# Time Complexity O(n),O(n^2),O(n^2) | Space Complexity O(1) | stable
def insertSort(array, begin=0, end=None):
    if end == None:
        end = len(array)
    for i in range(begin, end):
        j = i
        toChange = array[i]
        while (j != begin and array[j - 1] > toChange):
            array[j] = array[j - 1]
            j -= 1
        array[j] = toChange
    return array

1. Heap Sort 구현

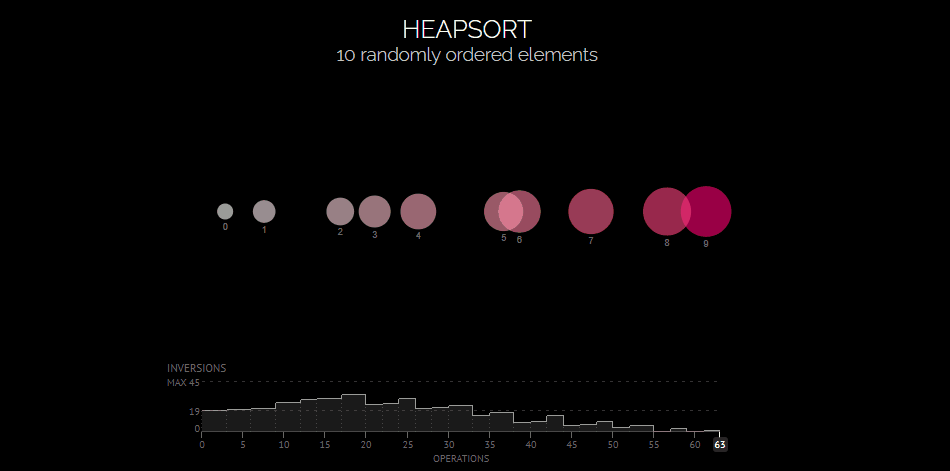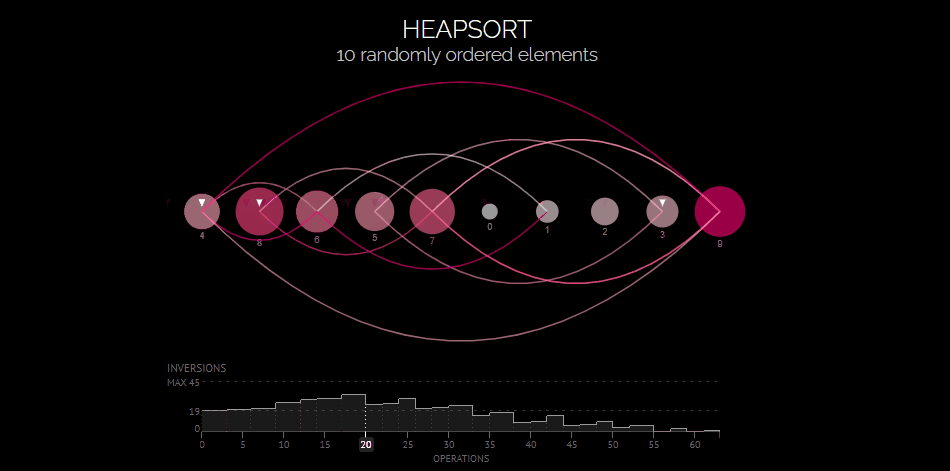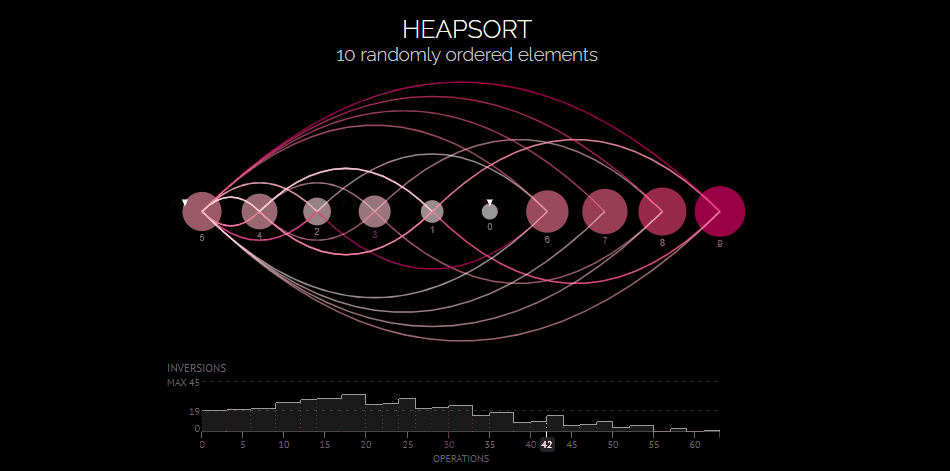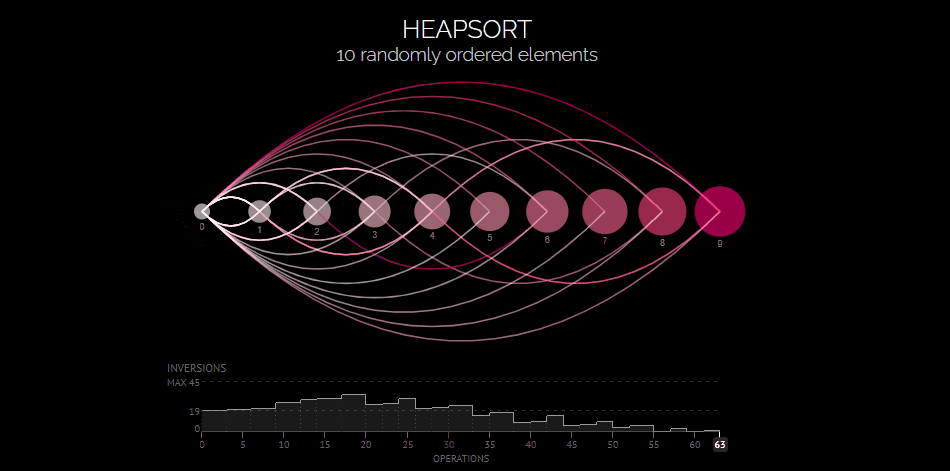
Heap Sort visualization

# Time Complexity O(nlogn) | Space Complexity O(1) | not stable
def heapify(arr, n, i):  # Max Heap
    largest = i  # 트리에서 가장 큰 값 찾기
    l = 2 * i + 1  # Left Node
    r = 2 * i + 2  # Right Node

    if l < n and arr[i] < arr[l]:
        largest = l

    if r < n and arr[largest] < arr[r]:
        largest = r

    # root가 최대가 아니면
    # 최대 값과 바꾸고, 계속 heapify
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)


def heapSort(arr):
    n = len(arr)

    for i in range(n // 2, -1, -1):
        heapify(arr, n, i)

    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        # Heapify root element
        heapify(arr, i, 0)
        
    return arr

2. pivot 값을 위한 median of 3 killer (배열의 시작, 중간, 끝), 함수 두개 중 맘에 드는 것을 선택

문자열을 정렬하게 못하게 됨.

# comparison보다 XOR을 속도면에서 선택함
def medianOf3(array, lowIdx, midIdx, highIdx):
    if ((array[lowIdx] > array[midIdx]) != (array[lowIdx] > array[highIdx])):
        return array[lowIdx]
    elif ((array[midIdx] > array[lowIdx]) != (array[midIdx] > array[highIdx])):
        return array[midIdx]
    else:
        return array[highIdx]
        
# 비교 줄이기 
def medianOf3(array, lowIdx, midIdx, highIdx):
   if (array[lowIdx] - array[midIdx]) * (array[highIdx] - array[lowIdx]) >= 0:
       return array[lowIdx]
   elif (array[midIdx] - array[lowIdx]) * (array[highIdx] - array[midIdx]) >= 0:
       return array[midIdx]
   else:
       return array[highIdx]

3. 파티션을 나누기 위한 getPartition 함수

def getPartition(array, low, high, pivot):
    i = low
    j = high
    while True:
        while (array[i] < pivot):
            i += 1
        j -= 1
        while (pivot < array[j]):
            j -= 1
        if i >= j:
            return i
        array[i], array[j] = array[j], array[i]
        i += 1

2. IntroSort(array)

# Time Complexity O(nlogn) | Space Complexity O(logn) | not stable
def introSort(array):
    maxDepth = 2 * (len(array).bit_length() - 1) # 2* (log2(length) - 1)
    sizeThreshold = 16
    return introSortHelper(array, 0, len(array), sizeThreshold, maxDepth)


def introSortHelper(array, start, end, sizeThreshold, depthLimit):
    # size가 16보다 크면 heap sort or quick sort
    while(end - start > sizeThreshold):
        if (depthLimit == 0):
            return heapSort(array)
        depthLimit -= 1

        median = medianOf3(array, start, start +
                           ((end - start) // 2) + 1, end - 1)
        p = getPartition(array, start, end, median)
        introSortHelper(array, p, end, sizeThreshold, depthLimit)
        end = p
    # insert Sort로 종료
    return insertSort(array, start, end)

 

3. 얼마나 빠른가?

테스트 배열을 3번 실행해서, 평균 정렬 시간을 출력하도록 했다.

크기 백만: 랜덤, 내림차순, 오름차순, 부분 정렬, k정렬

 

1. 랜덤한 숫자 1,000,000개 (Random) ( 3위 )

 

2. 거꾸로 정렬된 크기 1,000,000의 배열 (Descending) ( 3위 )

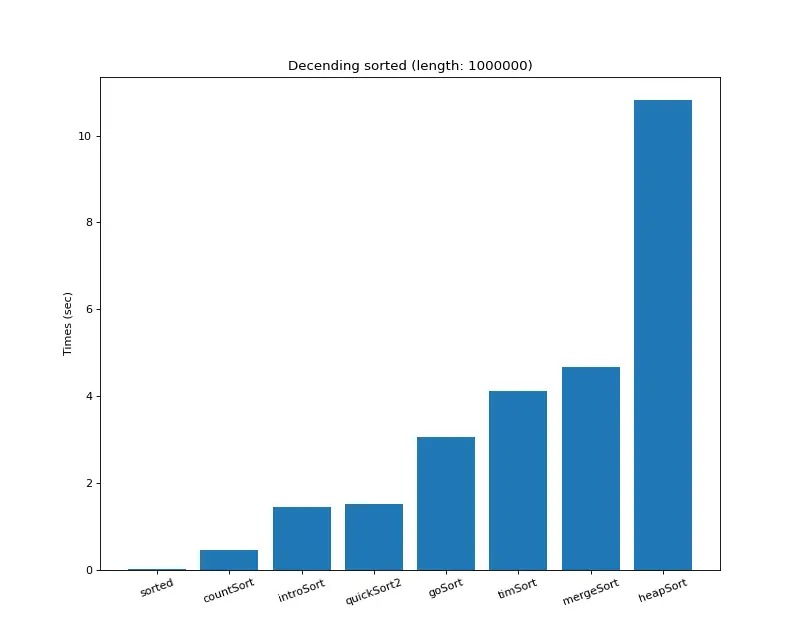
3. 정렬된 크기 1,000,000 배열 (Ascending) ( 3위 )

4. 크기 1,000,000의 부분 정렬된 랜덤 배열 ( 5위 )

5. 크기 1,000,000의 K정렬 ( 3위 )

 

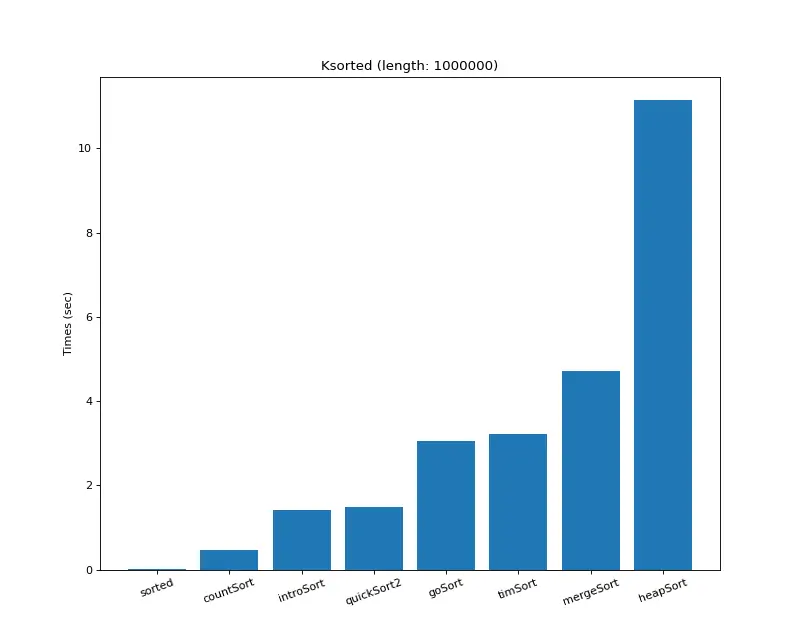
정렬 알고리즘 시간 복잡도 계산기: choiseokwon.tistory.com/231

풀 소스 확인 : https://gist.github.com/Alfex4936/62f81e9cde7719d4762f596068bfb001

Count Sort (https://choiseokwon.tistory.com/206)

TimSort (https://choiseokwon.tistory.com/208)

참고 : https://www.wikiwand.com/en/Introsort

참고 : https://www.geeksforgeeks.org/introsort-or-introspective-sort/