Python BFS(너비 탐색) 및 Iterative Deepening Depth-first Search

IDDFS

1. 소개

반복적 깊이 증가 (IDDFS)는 깊이 우선 탐색(DFS)처럼 메모리 필요량이 깊이 제한에 비례하면서도

최단 경로로 목표 노드를 찾는 것을 보장하는 방법이다.

IDDFS 방법에서는 목표 노드가 찾아질 때까지 깊이 제한을 1 씩 증가시키면서 연속적인 깊이 우선 탐색을 수행한다.

아래 그래프를 반복적 깊이 증가 탐색을 해보면 다음과 같다.

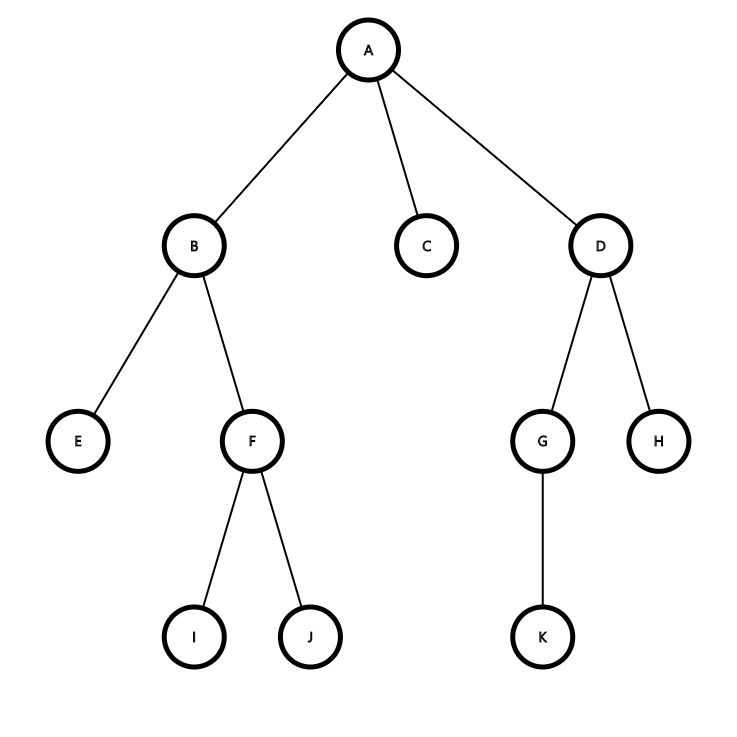
깊이 제한 1 = A -> B -> C -> D

깊이 제한 2 = A -> B -> E -> F -> C -> D -> G -> H

깊이 제한 3 = A -> B -> E-> F -> I -> J -> C -> D -> G -> H -> K

...

2. Node class

우선 Node 클래스를 만들어 준다.

class Node:
    def __init__(self, name):
        self.children = []
        self.name = name

    def addChild(self, nameList):
        for name in nameList:
            self.children.append(Node(name))
        return self

 

3. Make a graph with nodes

그다음, 그래프를 우선 만들어 준다.

graph = Node("A")
graph.addChild(["B", "C", "D"])
graph.children[0].addChild(["E", "F"])
graph.children[2].addChild(["G", "H"])
graph.children[0].children[1].addChild(["I", "J"])
graph.children[2].children[0].addChild(["K"])

 

4. BFS 구현

BFS(너비 우선 선택) 코드는 다음과 같다.

def breadthFirstSearch(self, result=[], que=[]):
    result.append(self.name)

    for i in self.children:
        que.append(i)

    while que:
        current = que.pop(0)
        current.breadthFirstSearch(result, que)

    return result

print(graph.breadthFirstSearch())

# ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K']

 

5. IDDFS

IDDFS, 반복적 깊이 증가 탐색은 우선 4가지 파라미터를 줄 것이다.

startNode (Node), target (str), currentDepth (int), maxDepth (int)

그리고, 이 예제에선 깊이를 +1이 아닌 x2 하여 계속 탐색할 것이다.

 

함수를 요약하면 :

IDDFS(타겟) : 깊이 = 1로 초기화하고, 최하단에 도달할 때까지, helper를 부르고, 깊이 *= 2를 해준다.)

IDDFS_HELPER(시작 노드, 타겟, 시작 탐색 깊이, 최대 탐색 깊이) : 자식들 모두 불러서 recursive 해준다.

def iterative_deepning_dfs(self, target):
    depth = 1
    bottom_reached = False
    while not bottom_reached:
        result, bottom_reached = self.iterative_deepning_dfs_helper(
            self, target, 0, depth)

        if result:
            print("Found")
            return result

        depth *= 2
        print(depth, 'increased')
    return None

def iterative_deepning_dfs_helper(self, node, target, currentDepth, maxDepth):
    """
    Args:
        node (Node): Node
        target (str): node.name을 비교함
        currentDepth (int): 시작 탐색 깊이
        maxDepth (int): 최대 탐색 깊이
    """
    print("Visiting", node.name)

    if node.name == target:
        return node, True

    if currentDepth == maxDepth:
        print("현재 최대 탐색 깊이 도달, 종료")
        if len(node.children) > 0:
            # 최하단까지 도달은 못했음
            return None, False
        else:
            return None, True

    # 자식들 모두 recursive
    bottom_reached = True
    for i in range(len(node.children)):
        result, bottom_reached_children = self.iterative_deepning_dfs_helper(
            node.children[i], target, currentDepth + 1,
            maxDepth)

        if result:
            return result, True

        bottom_reached = bottom_reached and bottom_reached_children

    return None, bottom_reached

 

결과

print(graph.iterative_deepning_dfs("K")) 를 실행하면 다음과 같다.

Visiting A
Visiting B
현재 최대 탐색 깊이 도달, 종료
Visiting C
현재 최대 탐색 깊이 도달, 종료
Visiting D
현재 최대 탐색 깊이 도달, 종료
2 increased
Visiting A
Visiting B
Visiting E
현재 최대 탐색 깊이 도달, 종료
Visiting F
현재 최대 탐색 깊이 도달, 종료
Visiting C
Visiting D
Visiting G
현재 최대 탐색 깊이 도달, 종료
Visiting H
현재 최대 탐색 깊이 도달, 종료
4 increased
Visiting A
Visiting B
Visiting E
Visiting F
Visiting I
Visiting J
Visiting C
Visiting D
Visiting G
Visiting K
Found
<__main__.Node object at 0x00000277E9C94348>