파이썬 A* (A-star) 최단 경로 찾기 알고리즘

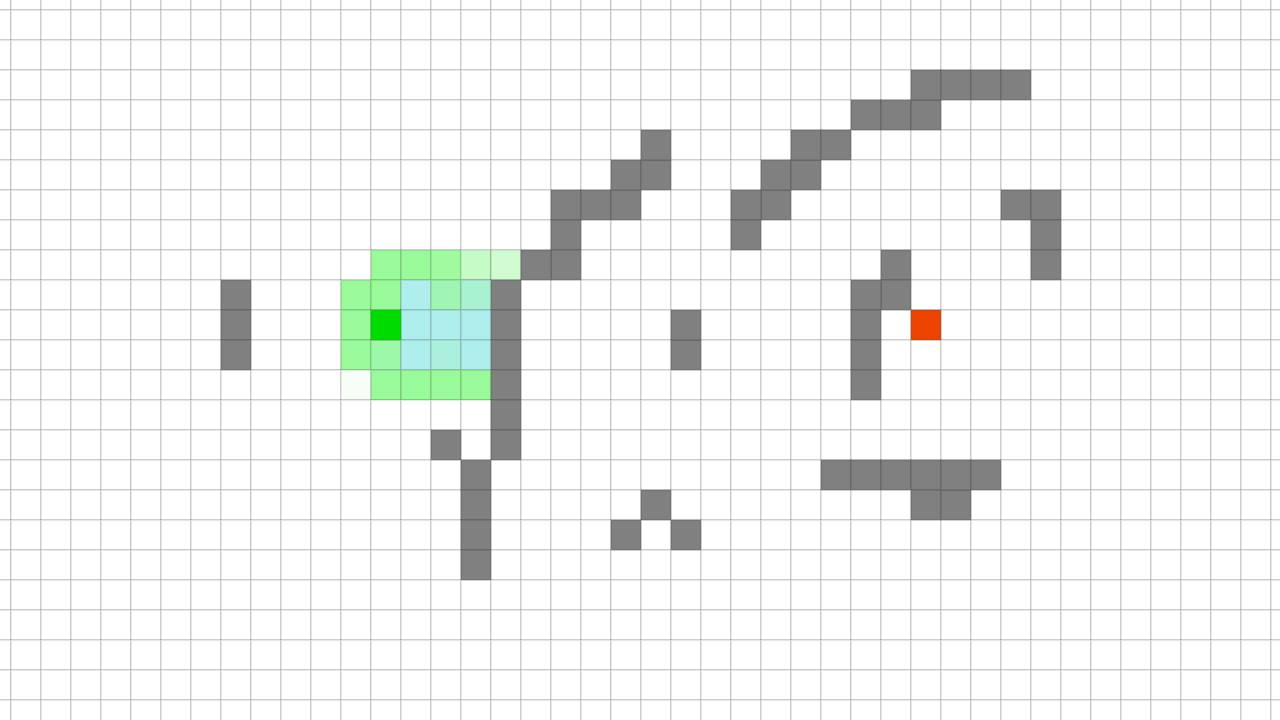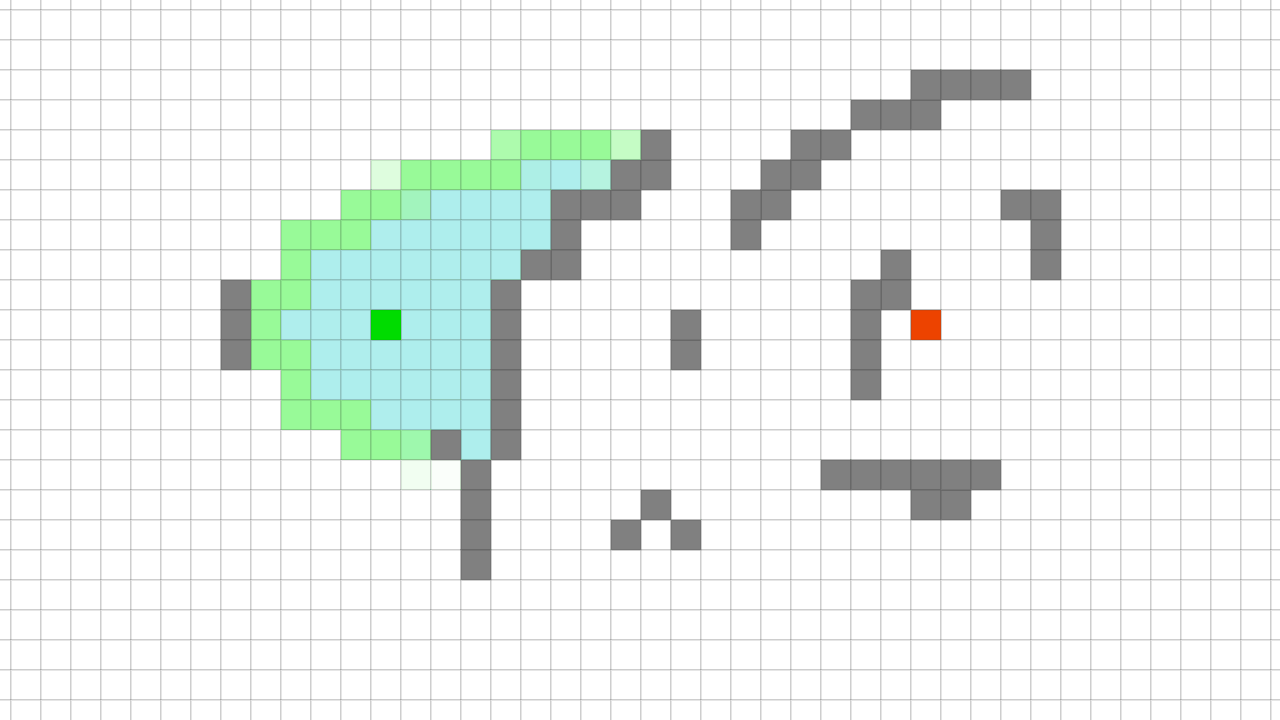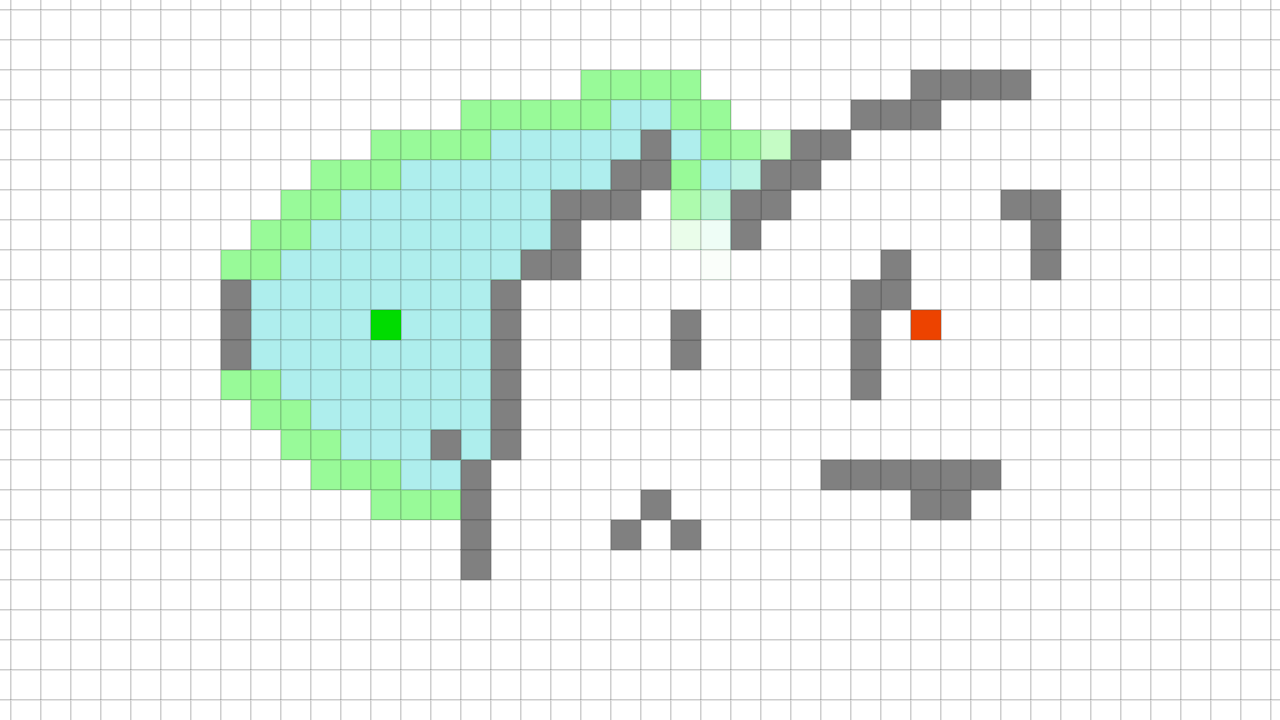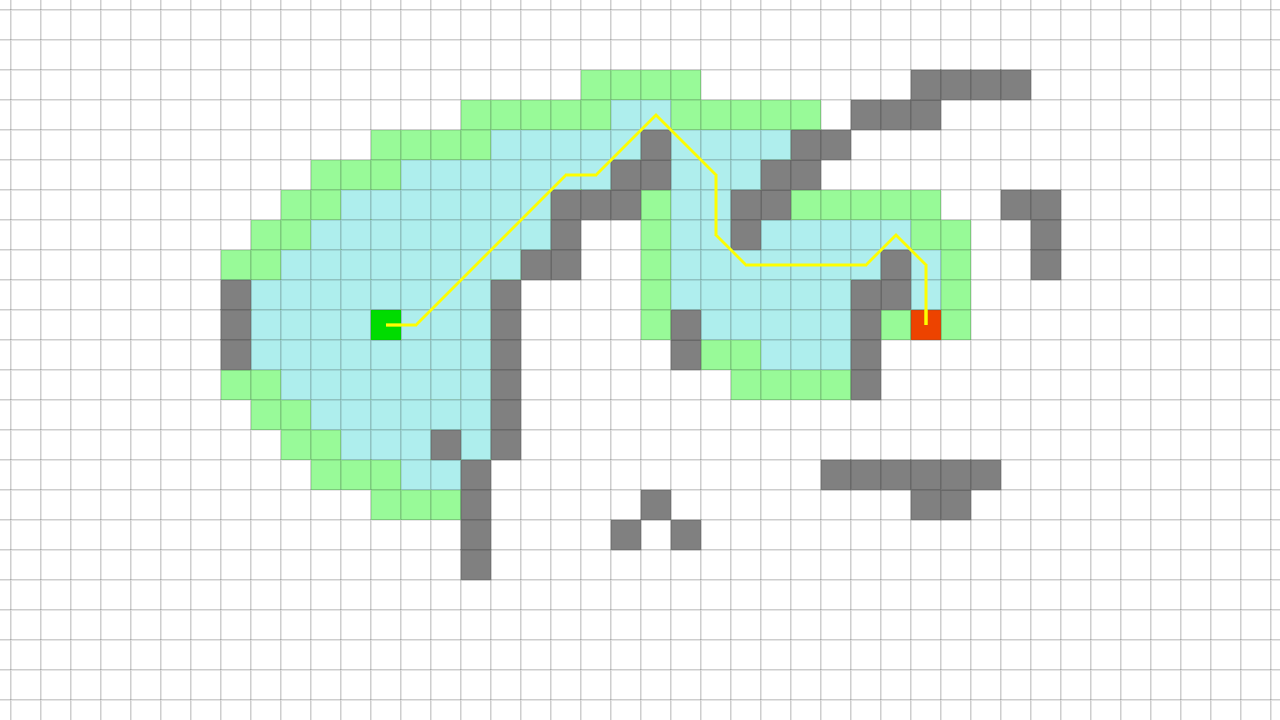
A* Pathfinding visualization

A* 길 찾기 알고리즘은 1968년에 Peter Hart, Nils Nilsson, Bertram Raphael에 의해 최초 공개됐다.

우선 Node 클래스는 아래와 같이 구현될 것이며, 아래 클래스를 보고 글을 읽으면 좀 더 편할 것이다.

class Node:
    def __init__(self, parent=None, position=None):
        self.parent = parent  # 이전 노드
        self.position = position  # 현재 위치

        self.f = 0
        self.g = 0
        self.h = 0

ex) 노드의 현재 위치는 xy좌표계를 사용한다.

start = (0, 0), end = (9,9)

aStar(star, end) -> Node(None, start)

 

 F = G + H 

우선 A* 알고리즘의 핵심 값인 F, G, H 값을 알아보겠다.

이 3개의 변수는 노드를 추가할 때마다 값이 갱신될 것이다.

• F = 출발 지점에서 목적지까지의 총 cost 합
• G = 현재 노드에서 출발 지점까지의 총 cost
• H = Heuristic(휴리스틱), 현재 노드에서 목적지까지의 추정 거리

Heuristic [휴리스틱]
형용사 (교수법·교육이) 체험적인 [스스로 발견하게 하는]

f, g, h 약자는 그냥 수학에서 $f(x), g(x), h(x)$이다.

 

이해를 돕기 위해, 아래 예제를 들어보겠다. (초록 점 = 시작, 빨간 점 = 종료)

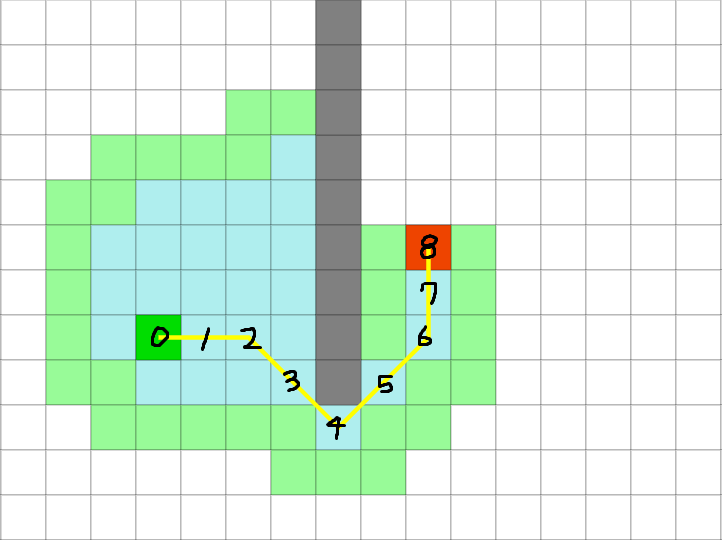
시작 노드를 node(0), 도착 노드를 node(8)

현재 노드가 node(2)라고 해보자.

 

 G(x) 

G = 현재 노드에서 출발 지점까지의 총 cost

현재 노드 = node(2), 출발 지점에서 2 cost만큼 떨어져 있다. (parent 노드는 당연히 node(1))

따라서, 현재 노드(2)는 아래와 같이 표현된다.

node(2).g = 2

 

 H(x) 

H = Heuristic(휴리스틱), 현재 노드에서 목적지까지의 추정 거리

현재 노드 = node(2) 에서 목적지까지의 거리를 추정해보자. (현재 노드부터 1이라고 가정)

5 cost만큼 오른쪽→으로 가서, 위↑로 3 cost만큼 가면 목적지 노드가 있다.

 

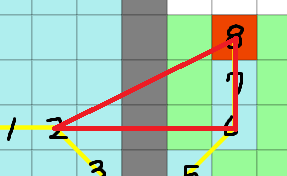
직각 삼각형의  빗변의  제곱이 두 직각변의 제곱의 합과 같다는 정리

여기서 피타고라스의 정리 $(a^2 + b^2 = c^2)$, 를  이용해서 H 값을 계산해보면,

node(2).h = $5^2 + 3^2$ = 34

$\sqrt{34}$로 지정하는 게 맞지만, 귀찮게 매번 계산 안 해도, 결과는 똑같이 나온다.하지만, 근접 거리나 값이 클 경우에는 다익지스트라처럼 작동할 수 있다.

 

파이썬으로는 아래와 같다. (맨해튼 거리)

child.h = ((child.position[0] - end_node.position[0]) ** 2) + \
          ((child.position[1] - end_node.position[1]) ** 2)

또는, 더 정확하게 하고 싶으면, octile distance + diagonal distance를 이용하면 된다.

def heuristic(node, goal, D=1, D2=2 ** 0.5):
    dx = abs(node.position[0] - goal.position[0])
    dy = abs(node.position[1] - goal.position[1])
    return D * (dx + dy) + (D2 - 2 * D) * min(dx, dy)
    
...
child.h = heuristic(child, endNode)
...

 

Heuristics 종류 : http://theory.stanford.edu/~amitp/GameProgramming/Heuristics.html

4방향으로 움직이면 보통, Manhatten Distance, 8방향으로 움직이면 Diagonal Distance

모든 방향은 Euclidean을 수정해서 사용하면 괜찮다. (맨해튼 거리가 제일 무난하다)

 

 F(x) 

F = 출발 지점에서 목적지까지의 총 cost 합

이제  현재 노드(node(2))의 G값과 H값을 더해보면,

node(2).f = node(2).g + node(2).h = 2 + 34 = 36

---

F 값 사용하기

F 값은 현재 노드가 목적지에 도달하는 데 있어서, 최선의 방법인지 확인할 수 있는 값이다.

이 F 값이 없으면, Dikjistra 길 찾기 알고리즘처럼 모든 노드에서 목적지까지 가는 방법을 찾는다.

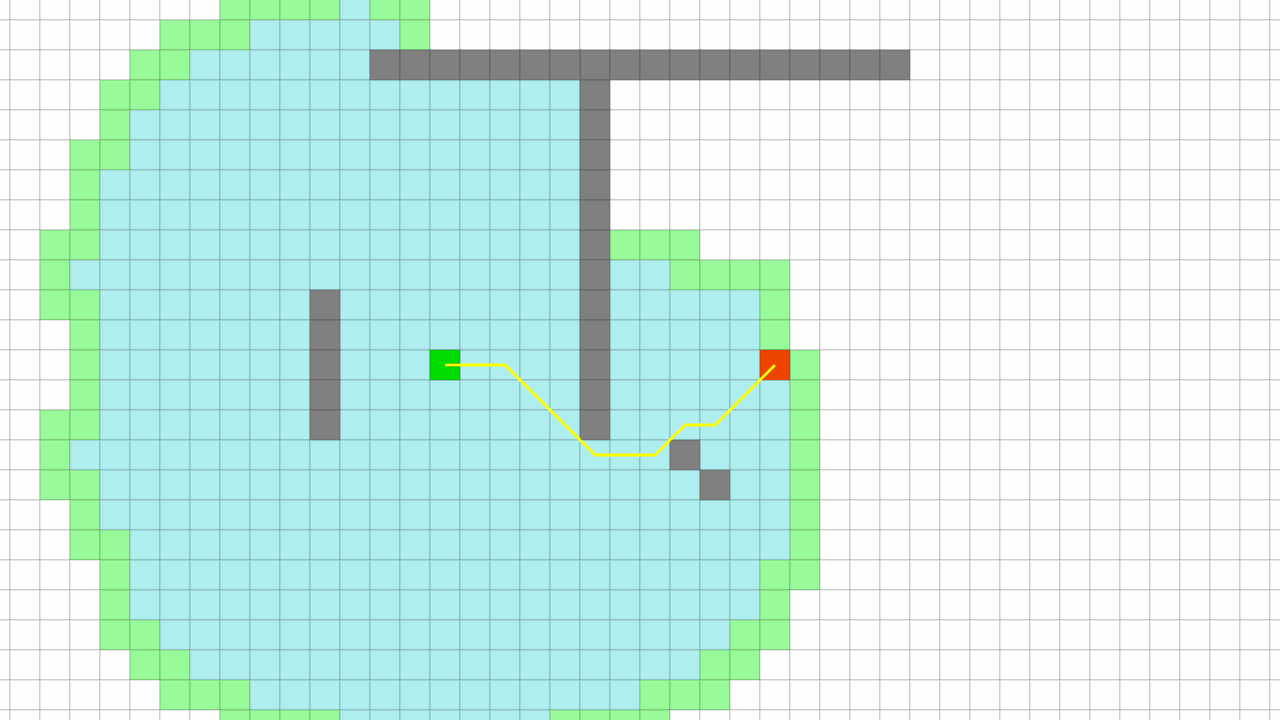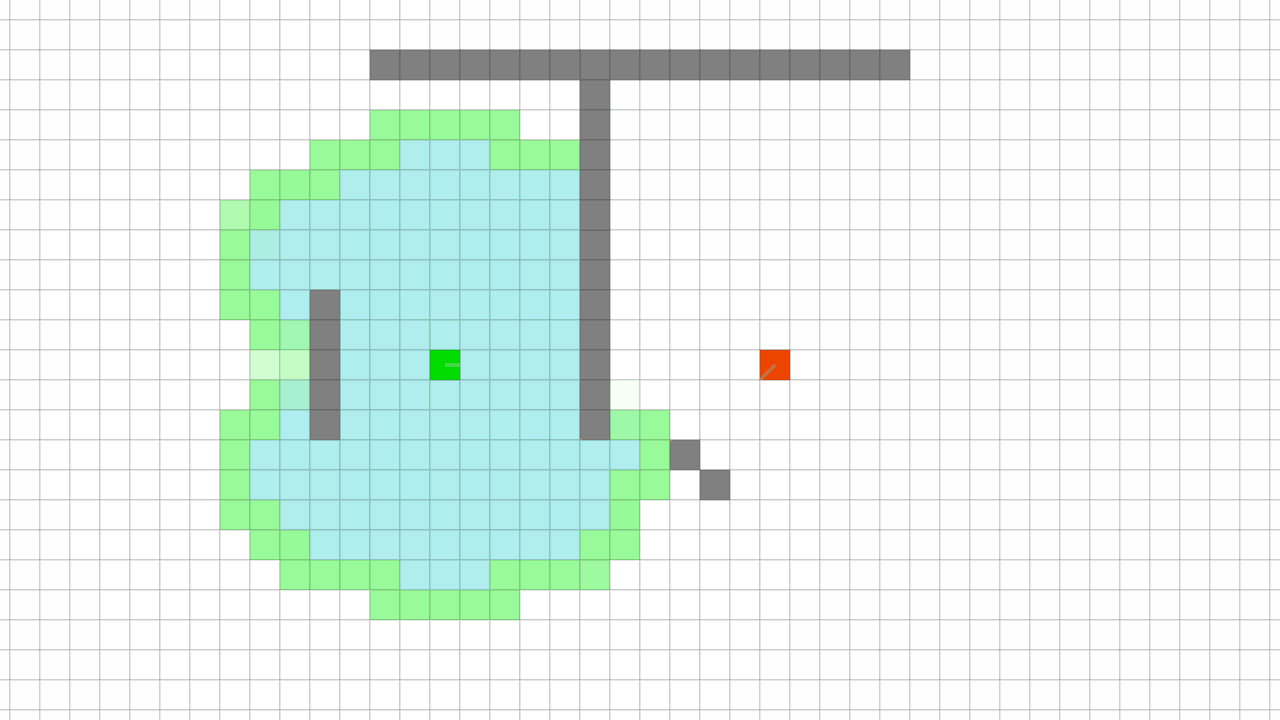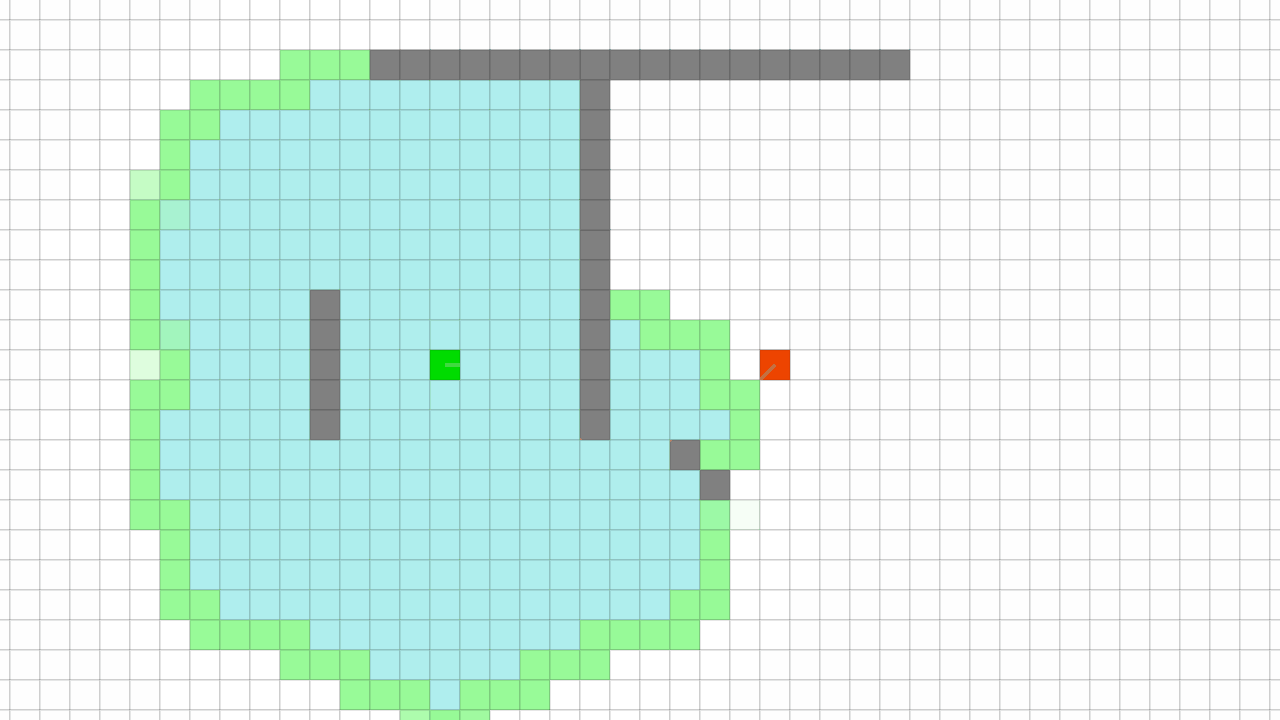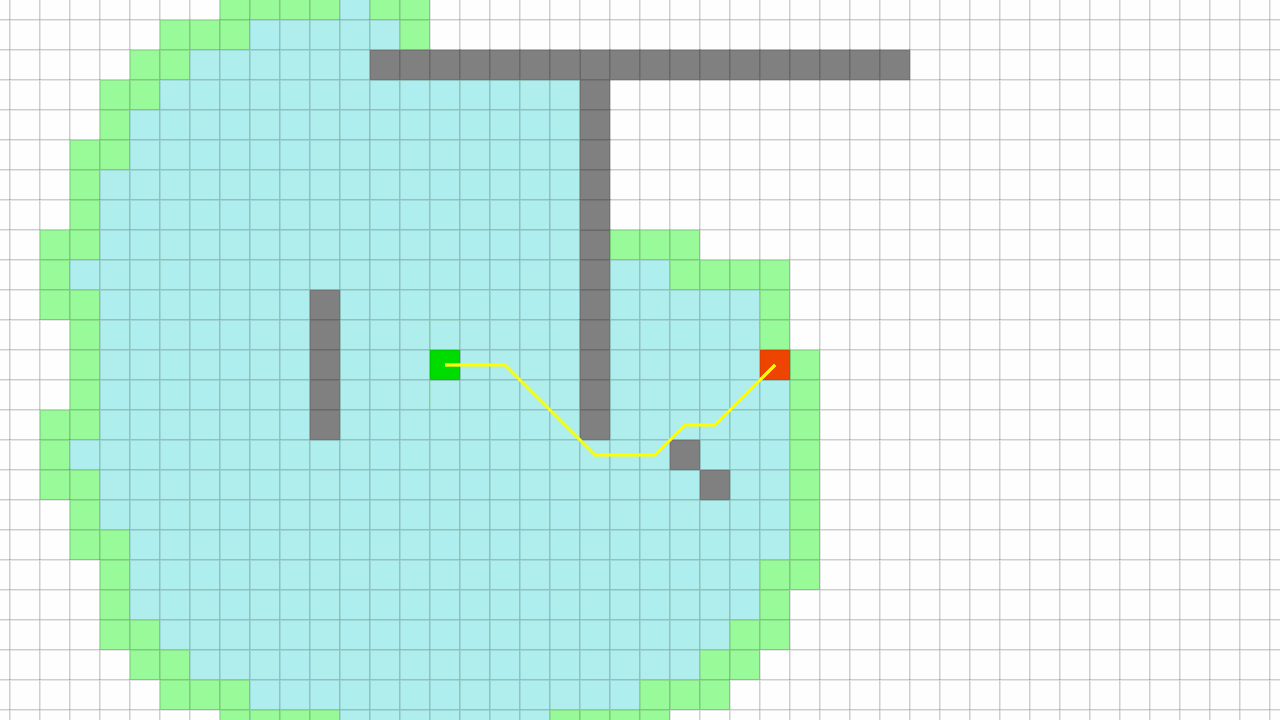
모든 노드에서 길을 찾는 다익지스트라 알고리즘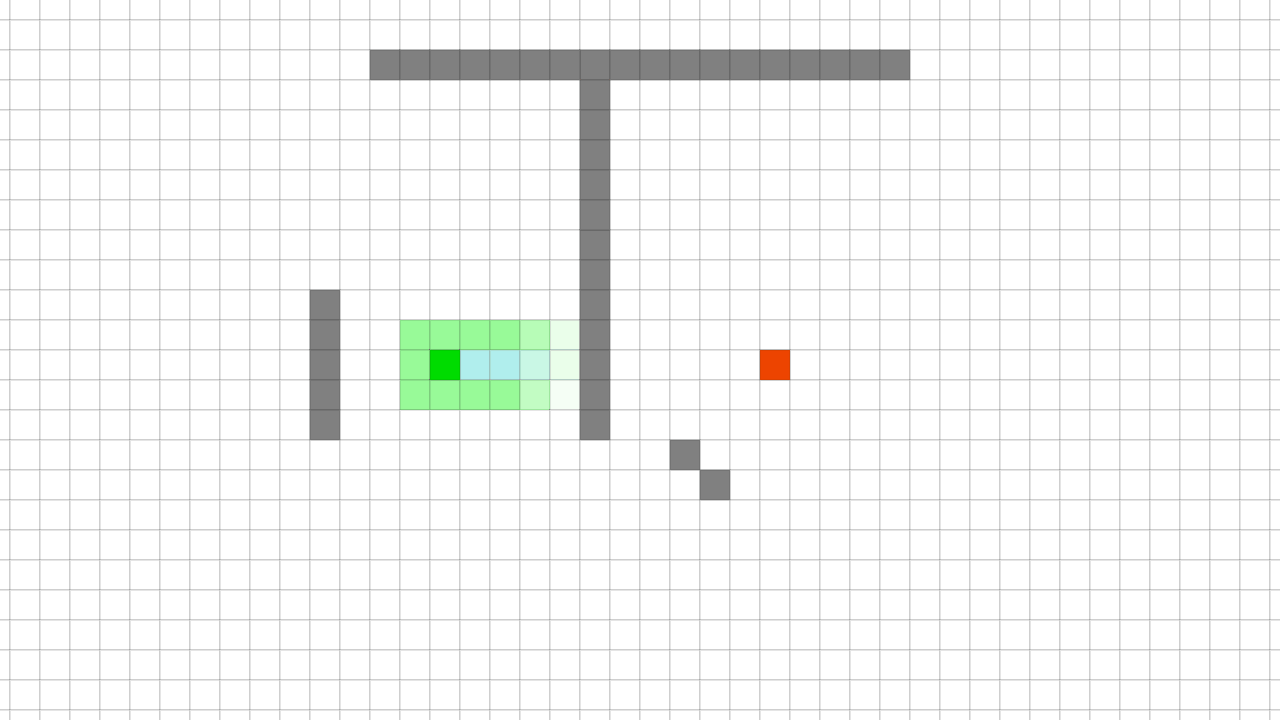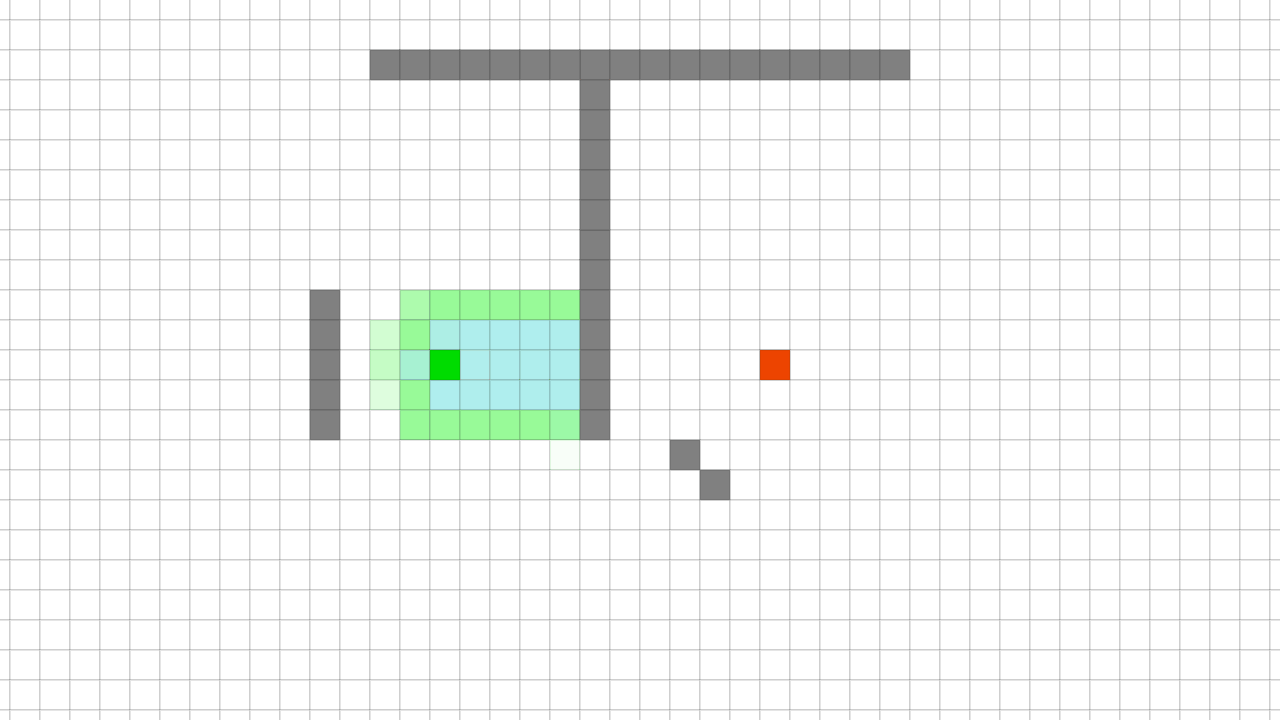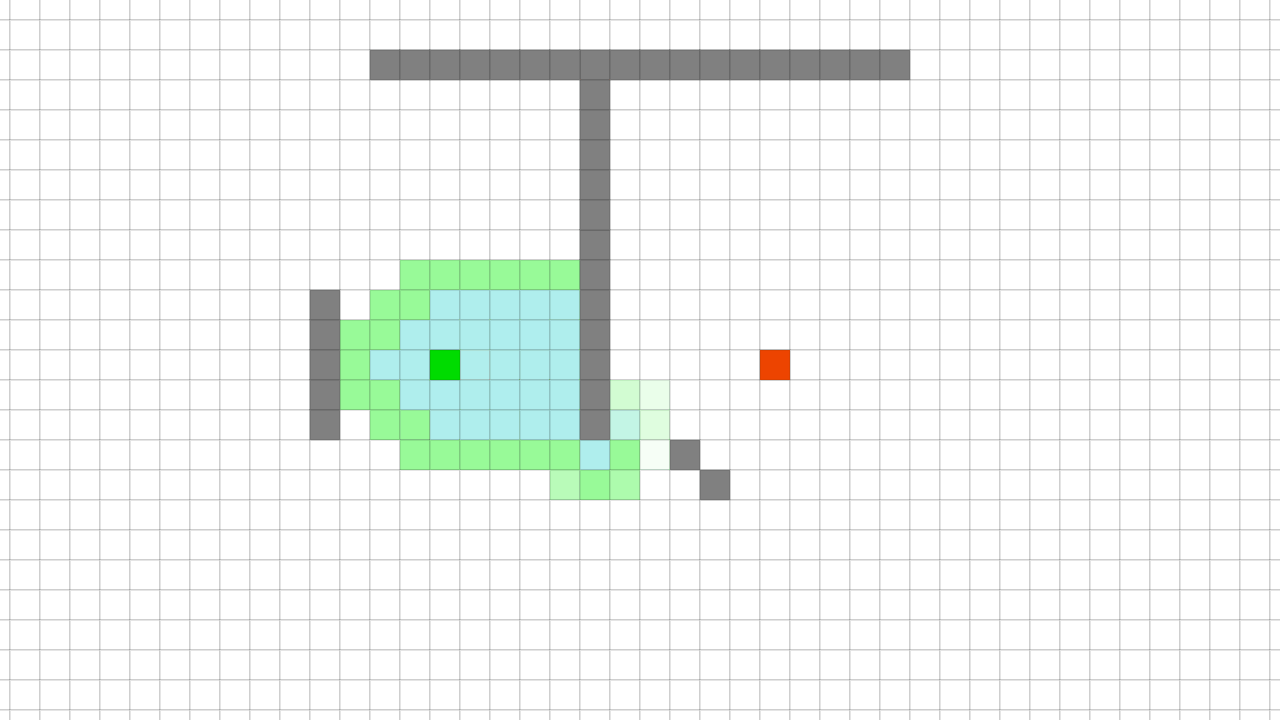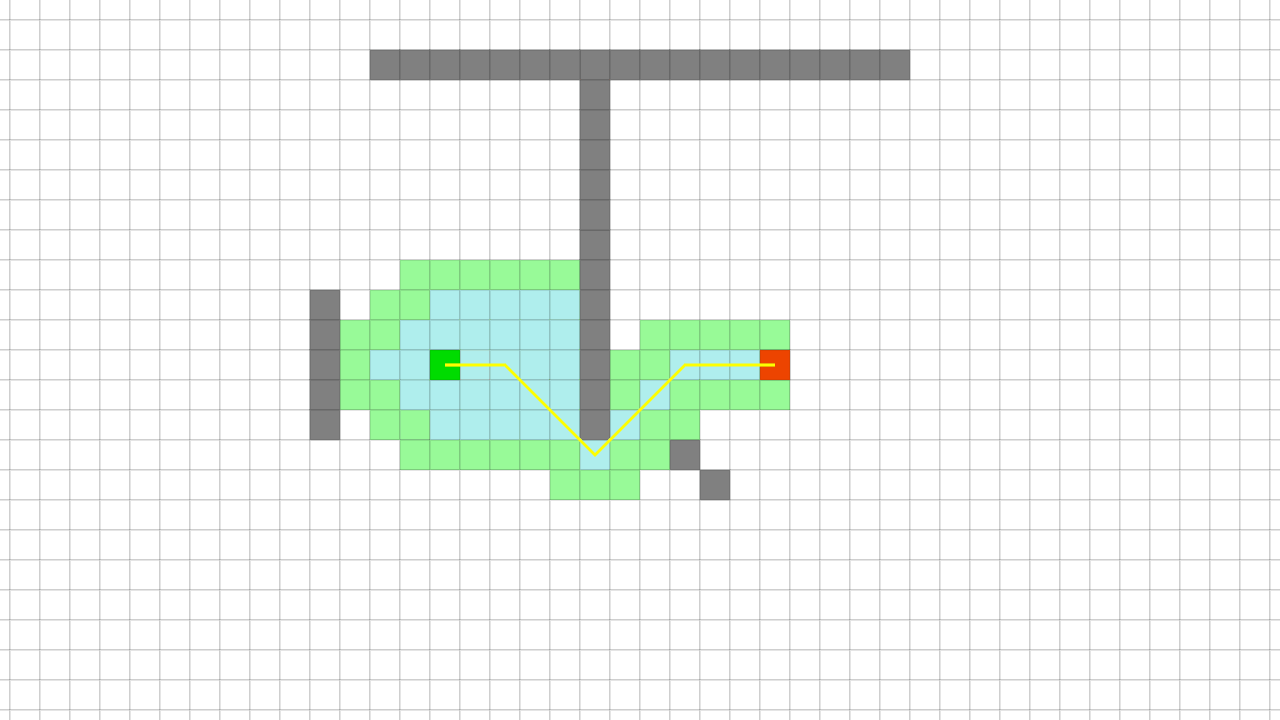

F 값을 이용해, 최선의 노드를 찾아 길을 찾는 A* 알고리즘

 

Pseudo Code

/* A* 특징
1. openList와 closeList라는 보조 데이터를 사용한다.
2. F = G + H 를 매번 노드를 생성할 때마다 계산한다.
3. openList에는 현재 노드에서 갈 수 있는 노드를 전부 추가해서 F,G,H를 계산한다.
    openList에 중복된 노드가 있다면, F값이 제일 작은 노드로 바꾼다.
    
4. closeList에는 openList에서 F값이 가장 작은 노드를 추가시킨다.
*/

openList.add(startNode)  # openList는 시작 노드로 init

while openList is not empty:
    # 현재 노드 = openList에서 F 값 가장 작은 것
    currentNode <- node in openList having the lowest F value
    openList.remove(currentNode)  # openList에서 현재 노드 제거
    closeList.add(currentNode)  # closeList에 현재 노드 추가
    
    if goalNode is currentNode:
        currentNode.parent.position 계속 추가 후
        경로 출력 후 종료
        
    children <- currentNode와 인접한 모든 노드 추가
    
    for each child in children:
        if child in closeList:
            continue
        
        child.g = currentNode.g + child와 currentNode 거리(1)
        child.h = child와 목적지까지의 거리
        child.f = child.g + child.h
        
        # child가 openList에 있고, child의 g 값이 openList에 중복된 노드 g값과 같으면
        # 다른 자식 불러오기
        if child in openList and child.g > openNode.g in openList:
            continue
            
        openList.add(child)
    

 

파이썬

길을 바꿔가며 테스트해본다.

# Time Complexity는 H에 따라 다르다.
# O(b^d), where d = depth, b = 각 노드의 하위 요소 수
# heapque를 이용하면 길을 출력할 때 reverse를 안해도 됨

import heapq  # priority queue

class Node:
    def __init__(self, parent=None, position=None):
        self.parent = parent
        self.position = position
        self.g = 0
        self.h = 0
        self.f = 0

    def __eq__(self, other):
        return self.position == other.position

    def __lt__(self, other):
        return self.f < other.f

def heuristic(node, goal, D=1, D2=2 ** 0.5):  # Diagonal Distance
    dx = abs(node.position[0] - goal.position[0])
    dy = abs(node.position[1] - goal.position[1])
    return D * (dx + dy) + (D2 - 2 * D) * min(dx, dy)

def aStar(maze, start, end):
    # startNode와 endNode 초기화
    startNode = Node(None, start)
    endNode = Node(None, end)

    # openList, closedList 초기화
    openList = []
    closedSet = set()

    # openList에 시작 노드 추가
    heapq.heappush(openList, startNode)

    # endNode를 찾을 때까지 실행
    while openList:
        # 현재 노드 지정
        currentNode = heapq.heappop(openList)
        closedSet.add(currentNode.position)

        # 현재 노드가 목적지면 current.position 추가하고
        # current의 부모로 이동
        if currentNode == endNode:
            path = []
            while currentNode is not None:
                path.append(currentNode.position)
                currentNode = currentNode.parent
            return path[::-1]

        # 인접한 xy좌표 전부, DFS
        for newPosition in (0, -1), (0, 1), (-1, 0), (1, 0), (-1, -1), (-1, 1), (1, -1), (1, 1):
            # 노드 위치 업데이트
            nodePosition = (currentNode.position[0] + newPosition[0], currentNode.position[1] + newPosition[1])

             # 미로 maze index 범위 안에 있어야함
            if nodePosition[0] > len(maze) - 1 or nodePosition[0] < 0 or nodePosition[1] > len(maze[0]) - 1 or nodePosition[1] < 0:
                continue

            # 장애물이 있으면 다른 위치 불러오기
            if maze[nodePosition[0]][nodePosition[1]] != 0:
                continue

            new_node = Node(currentNode, nodePosition)
            # 자식이 closedList에 있으면 continue
            if new_node.position in closedSet:
                continue

            # f, g, h값 업데이트
            new_node.g = currentNode.g + 1
            new_node.h = heuristic(new_node, endNode)
            new_node.f = new_node.g + new_node.h

            # 자식이 openList에 있으고, g값이 더 크면 continue
            # new_node.g >= child.g 로 하면 openList 중복성을 줄일 수도 있습니다.
            # 하지만 이건 시나리오에 따라 다르고, 대부분 엄격히 더 낮은 g 값을 확인하면 충분할 수 있습니다.
            if any(child for child in openList if new_node == child and new_node.g > child.g):
                continue

            heapq.heappush(openList, new_node)

def main():
    maze = [[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]

    start = (0, 0)
    end = (7, 6)

    path = aStar(maze, start, end)
    print(path)

if __name__ == '__main__':
    main()
    # [(0, 0), (1, 1), (2, 2), (3, 3), (4, 3), (5, 4), (6, 5), (7, 6)]

    # 실행 시간 : 0.0013초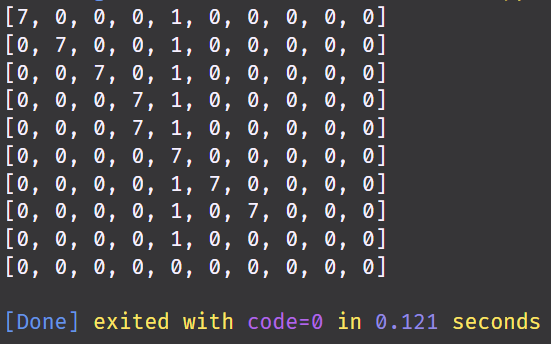

7 = 길

참고 지식 : https://en.wikipedia.org/wiki/A*_search_algorithm

참고 이미지 : https://qiao.github.io/PathFinding.js/visual/

참고 코드 : https://gist.github.com/Nicholas-Swift

그래프 표현 최단경로 찾기 (dijikstra) : https://choiseokwon.tistory.com/171?category=247927