Python QuickSort 최적화에 따른 속도

Quick Sort

인터넷에 있는 QuickSort 중 제일 빠른 방법은 무엇일까라는 생각이 들어

테스트를 진행해보았다. (big-O-calculator와 런타임으로 비교)

결과는 다를 수 있음

 

(페이스북 코딩 면접 중 한 문제는 quickSort 작성이었다.) - TechLead

0. 속도 테스트 코드

from bigO import BigO

lib = BigO()
size = 10_000

lib.test_all(quickSort)

lib.runtime(quickSort, "random", size)
lib.runtime(quickSort, "sorted", size)
lib.runtime(quickSort, "reversed", size)
lib.runtime(quickSort, "partial", size)
lib.runtime(quickSort, "Ksorted", size)

1. 기본 Quick Sort

def quickSort(array, low=0, high=None):
    if high is None:
        high = len(array) - 1

    if low < high:
        p = partition(array, low, high)
        quickSort(array, low, p)
        quickSort(array, p + 1, high)

    return array

파티션 기법에는 2가지가 유명한데, Lomuto나 Hoare 방법을 사용한다.

Hoare가 평균적으로 더 성능이 좋기 때문에 이 글에선 Hoare 파티션 기법만 이용하겠다.

def partition(array, low, high):
    pivot = array[(high + low) // 2]
    i = low - 1
    j = high + 1
    while True:
        i += 1
        while array[i] < pivot:
            i += 1
        j -= 1
        while array[j] > pivot:
            j -= 1

        if i >= j:
            return j

        array[i], array[j] = array[j], array[i]

1.1 테스트

테스트는 test_all 함수로 시간 복잡도 계산(3번 반복) 및 runtime(10,000 크기의 배열)을 이용했다.

모든 케이스 : O(nlog(n)) | 5개 케이스 평균 걸린 시간 : 0.023922

※ 결과는 다를 수 있음 ※

Running quickSort(tests)
Best : O(nlog(n)) Time
Average : O(nlog(n)) Time
Worst : O(nlog(n)) Time

Running quickSort(len 10000 random array)
Took 0.03053s to sort quickSort(random)

Running quickSort(len 10000 sorted array)
Took 0.01931s to sort quickSort(sorted)

Running quickSort(len 10000 reversed array)
Took 0.02026s to sort quickSort(reversed)

Running quickSort(len 10000 partial array)
Took 0.03032s to sort quickSort(partial)

Running quickSort(len 10000 ksorted array)
Took 0.01919s to sort quickSort(ksorted)

 

2. 기본 Quick Sort + Insertion Sort

def quickSort(array, low=0, high=None):
    if high is None:
        high = len(array) - 1

    if low < high and high - low > 16:
        p = partition(array, low, high)
        quickSort(array, low, p)
        quickSort(array, p + 1, high)

    return insertSort(array, low, high)
    
def partition(array, low, high):
    pivot = array[(high + low) // 2]
    i = low - 1
    j = high + 1
    while True:
        i += 1
        while array[i] < pivot:
            i += 1
        j -= 1
        while array[j] > pivot:
            j -= 1

        if i >= j:
            return j

        array[i], array[j] = array[j], array[i]


def insertSort(array, low=0, high=None):
    if high is None:
        high = len(array) - 1

    for i in range(low + 1, high + 1):
        j = i
        while j > 0 and array[j] < array[j - 1]:
            array[j], array[j - 1] = array[j - 1], array[j]
            j -= 1

    return array

거의 모든 하이브리드 정렬(timSort, Introspective Sort) 등에서 쓰이는 기법으로

16 정도의 작은 크기는 삽입 정렬이 가장 좋은 결과를 내기 때문에, 16 이하 사이즈면

insertSort로 return 시킨다.

 

2.1 테스트

테스트는 test_all 함수로 시간 복잡도 계산(3번 실행) 및 runtime(10,000 크기의 배열)을 이용했다.

모든 케이스 : O(nlog(n)) | 5개 케이스 평균 걸린 시간 : 0.03229

※ 결과는 다를 수 있음 (O(n) 가능) ※

Running quickSort(tests)
Best : O(nlog(n)) Time
Average : O(nlog(n)) Time
Worst : O(nlog(n)) Time

Running quickSort(len 10000 random array)
Took 0.04642s to sort quickSort(random)

Running quickSort(len 10000 sorted array)
Took 0.02323s to sort quickSort(sorted)

Running quickSort(len 10000 reversed array)
Took 0.02424s to sort quickSort(reversed)

Running quickSort(len 10000 partial array)
Took 0.04394s to sort quickSort(partial)

Running quickSort(len 10000 ksorted array)
Took 0.02362s to sort quickSort(ksorted)

 

3. tail recursion + Insertion Sort

def quickSort(array, low=0, high=None):
    if high is None:
        high = len(array) - 1
    stack = []
    stack.append((low, high))
    while stack:
        low, high = stack.pop()
        if high - low > 16:
            q = partition(array, low, high)
            stack.append((q + 1, high))
            stack.append((low, q))
        elif low < high:
            insertSort(array, low, high)
    return array


def partition(array, low, high):
    pivot = array[(high + low) // 2]
    # pivot = array[randint(low, high)]
    i = low - 1
    j = high + 1
    while True:
        i += 1
        while array[i] < pivot:
            i += 1
        j -= 1
        while array[j] > pivot:
            j -= 1

        if i >= j:
            return j

        array[i], array[j] = array[j], array[i]


def insertSort(array, low=0, high=None):
    if high is None:
        high = len(array) - 1

    for i in range(low + 1, high + 1):
        j = i
        while j > 0 and array[j] < array[j - 1]:
            array[j], array[j - 1] = array[j - 1], array[j]
            j -= 1

    return array

꼬리 재귀 및 Insertion Sort 합치기

 

3.1 테스트

테스트는 test_all 함수로 시간 복잡도 계산(3번 반복) 및 runtime(10,000 크기의 배열)을 이용했다.

모든 케이스 : O(nlog(n)) | 5개 케이스 평균 걸린 시간 : 0.01230

※ 결과는 다를 수 있음 ※

Running quickSort(tests)
Best : O(nlog(n)) Time
Average : O(nlog(n)) Time
Worst : O(nlog(n)) Time

Running quickSort(len 10000 random array)
Took 0.02814s to sort quickSort(random)

Running quickSort(len 10000 sorted array)
Took 0.01070s to sort quickSort(sorted)

Running quickSort(len 10000 reversed array)
Took 0.01174s to sort quickSort(reversed)

Running quickSort(len 10000 partial array)
Took 0.02655s to sort quickSort(partial)

Running quickSort(len 10000 ksorted array)
Took 0.01094s to sort quickSort(ksorted)

 

4. Recursive + Random pivot

def quickSort(array):
    if len(array) <= 1:
        return array

    pivot = array[randrange(0, len(array))]
    less = []
    equal = []
    great = []

    for x in array:
        if x == pivot:
            equal.append(x)
        elif x > pivot:
            great.append(x)
        else:
            less.append(x)

    return quickSort(less) + equal + quickSort(great)

보통 첫 번째, 마지막이나 중간으로 피봇을 선택하는 방식은 O(n^2)이 나올 수 있는데,

완전 랜덤 하게 하면 이 케이스는 해결된다.

 

4.1 테스트

테스트는 test_all 함수로 시간 복잡도 계산(3번 반복) 및 runtime(10,000 크기의 배열)을 이용했다.

모든 케이스 : O(nlog(n)) | 5개 케이스 평균 걸린 시간 : 0.03271

※ 결과는 다를 수 있음 ※

Running quickSort(tests)
Best : O(nlog(n)) Time
Average : O(nlog(n)) Time
Worst : O(nlog(n)) Time

Running quickSort(len 10000 random array)
Took 0.03054s to sort quickSort(random)

Running quickSort(len 10000 sorted array)
Took 0.03833s to sort quickSort(sorted)

Running quickSort(len 10000 reversed array)
Took 0.03435s to sort quickSort(reversed)

Running quickSort(len 10000 partial array)
Took 0.02926s to sort quickSort(partial)

Running quickSort(len 10000 ksorted array)
Took 0.03111s to sort quickSort(ksorted)

 

5. Recursive + Random pivot + 삽입 정렬

def quickSort(array):
    if len(array) <= 16:
        return insertSort(array)

    pivot = array[randrange(0, len(array))]
    less = []
    equal = []
    great = []

    for x in array:
        if x == pivot:
            equal.append(x)
        elif x > pivot:
            great.append(x)
        else:
            less.append(x)

    return quickSort(less) + equal + quickSort(great)

보통 첫 번째, 마지막이나 중간으로 피봇을 선택하는 방식은 O(n^2)이 나올 수 있는데,

완전 랜덤 하게 하면 이 케이스는 해결된다.

 

5.1 테스트

테스트는 test_all 함수로 시간 복잡도 계산(3번 반복) 및 runtime(10,000 크기의 배열)을 이용했다.

모든 케이스 : O(nlog(n)) | 5개 케이스 평균 걸린 시간 : 0.02615

※ 결과는 다를 수 있음 ※

Running quickSort(tests)
Best : O(nlog(n)) Time
Average : O(nlog(n)) Time
Worst : O(nlog(n)) Time

Running quickSort(len 10000 random array)
Took 0.02887s to sort quickSort(random)

Running quickSort(len 10000 sorted array)
Took 0.02113s to sort quickSort(sorted)

Running quickSort(len 10000 reversed array)
Took 0.03361s to sort quickSort(reversed)

Running quickSort(len 10000 partial array)
Took 0.02609s to sort quickSort(partial)

Running quickSort(len 10000 ksorted array)
Took 0.02105s to sort quickSort(ksorted)

 

6. Median of three

def partition(array, low, high):
    pivot = median_of_three(array, low, high)
    i = low - 1
    j = high + 1
    while True:
        i += 1
        while array[i] < pivot:
            i += 1
        j -= 1
        while array[j] > pivot:
            j -= 1

        if i >= j:
            return j

        array[i], array[j] = array[j], array[i]


def median_of_three(array, low, high):
    mid = (low + high - 1) // 2
    if (array[low] - array[mid]) * (array[high] - array[low]) >= 0:
        return array[low]
    elif (array[mid] - array[low]) * (array[high] - array[mid]) >= 0:
        return array[mid]
    else:
        return array[high]


def quickSort(array, low=0, high=None):
    if high is None:
        high = len(array) - 1

    while low < high and high - low > 16:
        q = partition(array, low, high)
        quickSort(array, low, q)
        low = q + 1

    return insertSort(array, low, high)

Median of three + Insertion Sort + Tail recursive + Hoare 파티션

 

6.1 테스트

테스트는 test_all 함수로 시간 복잡도 계산(3번 반복) 및 runtime(10,000 크기의 배열)을 이용했다.

모든 케이스 : O(nlog(n)) | 5개 케이스 평균 걸린 시간 : 0.018816

※ 결과는 다를 수 있음 ※

Running quickSort(tests)
Best : O(nlog(n)) Time
Average : O(nlog(n)) Time
Worst : O(nlog(n)) Time

Running quickSort(len 10000 random array)
Took 0.02966s to sort quickSort(random)

Running quickSort(len 10000 sorted array)
Took 0.01186s to sort quickSort(sorted)

Running quickSort(len 10000 reversed array)
Took 0.01346s to sort quickSort(reversed)

Running quickSort(len 10000 partial array)
Took 0.02741s to sort quickSort(partial)

Running quickSort(len 10000 ksorted array)
Took 0.01169s to sort quickSort(ksorted)

 

7. 결과

3번 > 6번 > 1번 > 5번 > 2번 > 4번

 

7.1 피봇 선택에 따른 속도 변화

제일 빠르게 나온 3번 Quick Sort를 기준으로, 총 4개의 피봇 선택 방식을 테스트.

1. 항상 중간 값

2. Median-of-3-killer (중간 값 찾기)

3. Random median-of-3-killer (랜덤 인덱스 중 중간 값 찾기)

4. 1번 메소드에서 시작~끝 사이 중 랜덤 값

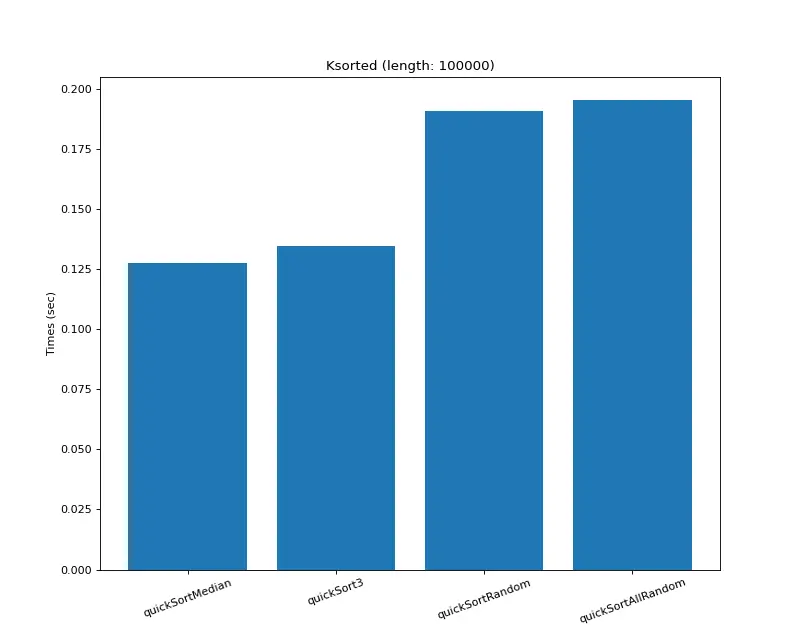
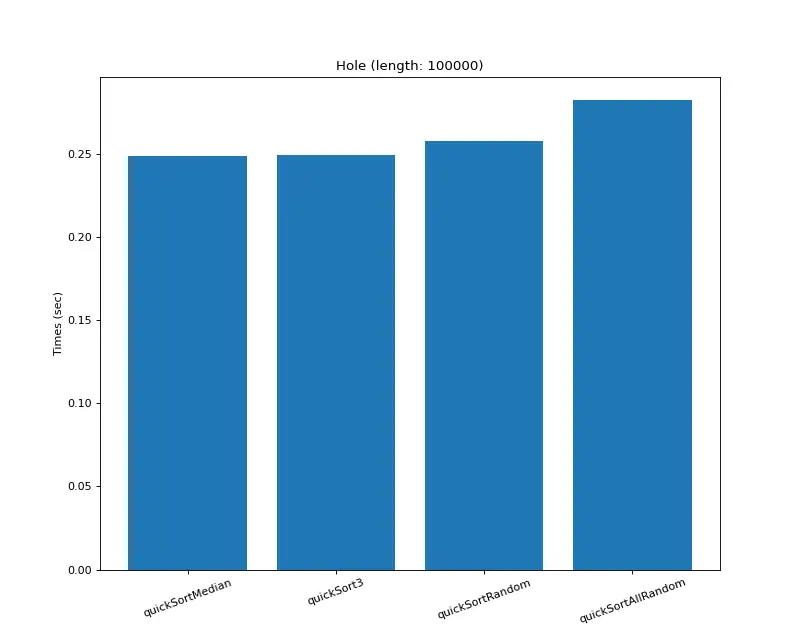
def quickSortMedian(array):
    ...
    pivot = array[(high + low) // 2]
    ...


def quickSort3(array):
    ...
    pivot = medianOf3(array, low, (low + high) // 2, high)
    ...


def quickSortAllRandom(array):
    ...
    pivot = medianOf3(
            array, randint(low, high), randint(low, high), randint(low, high)
        )
    ...


def quickSortRandom(array):
    ...
    pivot = array[randint(low, high)]
    ...
    

def medianOf3(array, lowIdx, midIdx, highIdx):
    if (array[lowIdx] - array[midIdx]) * (array[highIdx] - array[lowIdx]) >= 0:
        return array[lowIdx]

    elif (array[midIdx] - array[lowIdx]) * (array[highIdx] - array[midIdx]) >= 0:
        return array[midIdx]

    else:
        return array[highIdx]

 

테스트 배열 (8개, 크기=십만)

랜덤 배열, 내림차순 정렬 배열, 오름차순 정렬 배열, 부분 정렬 배열,

K정렬 배열, 모든 값 같은 배열, 모든 값이 거의 비슷한 배열, 하나의 요소만 다른 배열

(생성기는 big-O-calculator 이용)

(결과: 중간 값이 제일 빨랐음)

 

참고 위키백과 : en.wikipedia.org/wiki/Quicksort