파이썬 go-lang sort() 구현

go-lang.sort()

golang/go

 

1. 소개

Go언어의 기본 정렬은 quickSort 변형을 사용하고 있다.

계산해보면, 시간 복잡도는 모든 상황에서 $O(nlog(n))$ | 공간 복잡도는 $O(1)$

 

Pseudo Code

# Go Sort
 
procedure sort(A : array):
    let maxdepth = log2(length(A) - 1) × 2
    quickSort(A, 0, len(A), maxdepth)

procedure quickSort(A, a, b, maxdepth):
    n ← b - a
    
    while n ≥ 12:
    	if maxdepth = 0:
            return heapsort(A)
            
        maxDepth--
        
        low, high ← pivot
        quickSort(a, p)
        quickSort(p, b)
    else if n ≥ 1:
    	# Gap 6, shellSort
    	for i in range(a + 6, b):
            if A[i] < A[i - 6]:
                A[i], A[i - 6] = A[i - 6], A[i]

    return insertSort(A, a, b)

 

2. 구현

goSort

def goSort(array):
    maxDepth = 2 * (len(array).bit_length() - 1)  # 2 * log2(len) - 1과 같음
    quickSort(array, 0, len(array), maxDepth)
    return array

 

QuickSort

def quickSort(array, a, b, maxDepth):
    while b - a > 12:  # Use ShellSort for slices <= 12 elements
        if maxDepth == 0:
            return heapSort(array, a, b)

        maxDepth -= 1
        mlo, mhi = doPivot(array, a, b)
        # Avoiding recursion on the larger subproblem guarantees
        # a stack depth of at most lg(b-a).
        if mlo - a < b - mhi:
            quickSort(array, a, mlo, maxDepth)
            a = mhi  # i.e., quickSort(array, mhi, b)
        else:
            quickSort(array, mhi, b, maxDepth)
            b = mlo  # i.e., quickSort(array, a, mlo)

    if b - a > 1:
        # Do ShellSort pass with gap 6
        # It could be written in this simplified form cause b-a <= 12
        for i in range(a + 6, b):
            if array[i] < array[i - 6]:
                array[i], array[i - 6] = array[i - 6], array[i]

        return insertSort(array, a, b)

 

Pivot chooser

Lomuto의 파티션 기법을 기반으로, protect를 걸어 필요 이상으로 계산하는 것을 줄인 것 같다.

def doPivot(array, lo, hi):
    m = int(unsigned(lo + hi) >> 1)

    if hi - lo > 40:
        # Tukey's ``Ninther,'' median of three medians of three.
        s = (hi - lo) // 8
        medianOfThree(array, lo, lo + s, lo + 2 * s)
        medianOfThree(array, m, m - s, m + s)
        medianOfThree(array, hi - 1, hi - 1 - s, hi - 1 - 2 * s)

    medianOfThree(array, lo, m, hi - 1)

    pivot = lo
    a, c = lo + 1, hi - 1

    while a < c and array[a] < array[pivot]:
        a += 1
    b = a
    while True:
        while b < c and array[pivot] >= array[b]:
            b += 1
        while b < c and array[pivot] < array[c - 1]:
            c -= 1
        if b >= c:
            break

        array[b], array[c - 1] = array[c - 1], array[b]
        b += 1
        c -= 1

    protect = hi - c < 5
    if not protect and hi - c < (hi - lo) // 4:
        dups = 0
        if array[pivot] >= array[hi - 1]:
            array[c], array[hi - 1] = array[hi - 1], array[c]
            c += 1
            dups += 1
        if array[b - 1] >= array[pivot]:
            b -= 1
            dups += 1

        if array[m] >= array[pivot]:
            array[m], array[b - 1] = array[b - 1], array[m]
            b -= 1
            dups += 1

        protect = dups > 1

    if protect:
        while True:
            while a < b and array[b - 1] >= array[pivot]:
                b -= 1
            while a < b and array[a] < array[pivot]:
                a += 1
            if a >= b:
                break

            array[a], array[b - 1] = array[b - 1], array[a]
            a += 1
            b -= 1

    array[pivot], array[b - 1] = array[b - 1], array[pivot]
    return b - 1, c

 

Median-Of-Three

a <= b <= c 로 만듦

John Tukey's nInther

def medianOfThree(array, m1, m0, m2):
        # sort 3 elements
        if array[m1] < array[m0]:
            array[m1], array[m0] = array[m0], array[m1]

        # data[m0] <= data[m1]
        if array[m2] < array[m1]:
            array[m2], array[m1] = array[m1], array[m2]

            # data[m0] <= data[m2] && data[m1] < data[m2]
            if array[m1] < array[m0]:
                array[m1], array[m0] = array[m0], array[m1]

        # now data[m0] <= data[m1] <= data[m2]

 

Heap Sort 및 Insertion Sort

def insertSort(array, begin=0, end=None):
    if end == None:
        end = len(array)
    for i in range(begin, end):
        j = i
        toChange = array[i]
        while j != begin and array[j - 1] > toChange:
            array[j] = array[j - 1]
            j -= 1
        array[j] = toChange
    return array

def siftDown(array, lo, hi, first):
    root = lo
    while True:
        child = 2 * root + 1
        if child >= hi:
            break

        if child + 1 < hi and array[first + child] < array[first + child + 1]:
            child += 1

        if array[first + root] >= array[first + child]:
            return

        array[first + root], array[first + child] = (
            array[first + child],
            array[first + root],
        )
        root = child

def heapSort(array, a, b):
    first = a
    lo = 0
    hi = b - a

    # Build heap with greatest element at top.
    for i in range((hi - 1) // 2, -1, -1):
        siftDown(array, i, hi, first)

    # Pop elements, largest first, into end of data.
    for i in range(hi - 1, -1, -1):
        array[first], array[first + i] = array[first + i], array[first]
        siftDown(array, lo, i, first)

 

3. 결과

크기 10,000 랜덤 배열 (6위)

array = [randint(-10000, 10000) for i in range(10000)]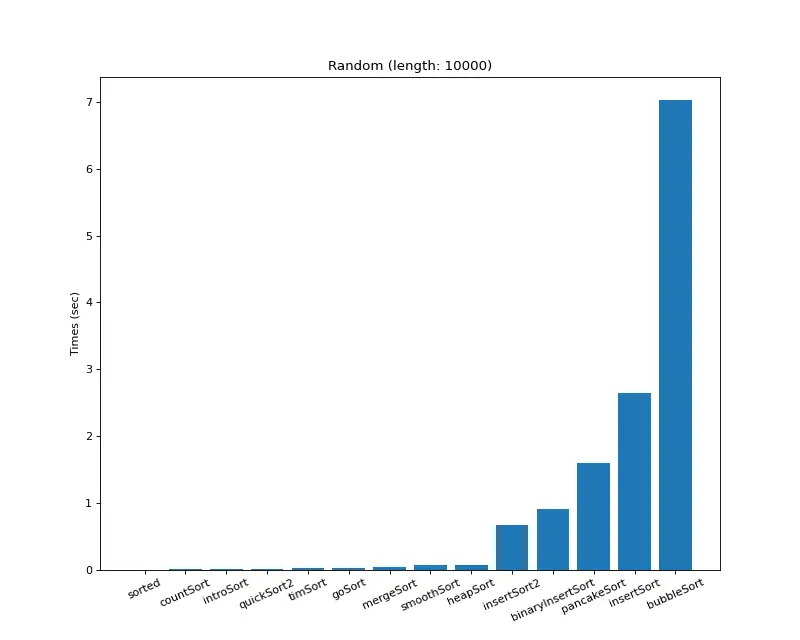

크기 10,000 정렬된 배열 (8위)

array = [i for i in range(10000)]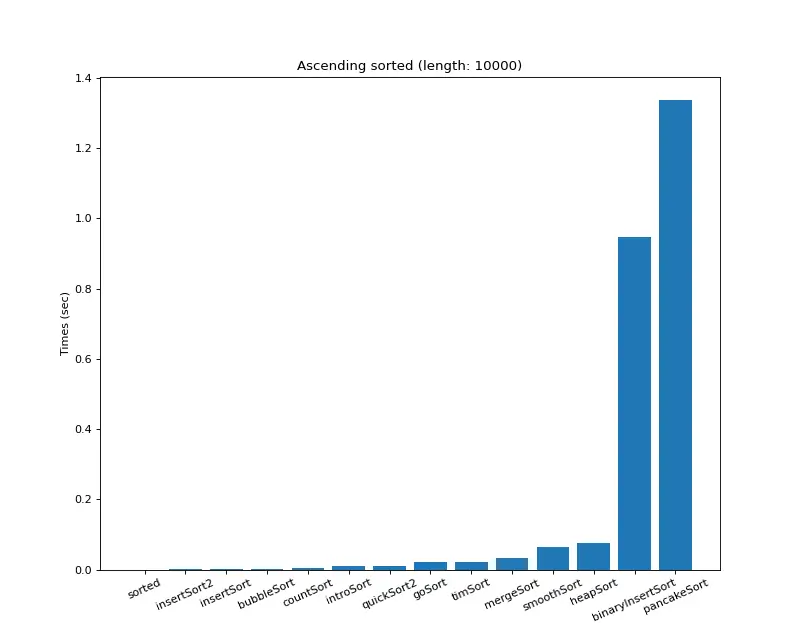

크기 10,000 내림차순 정렬된 배열 (5위)

array = [i for i in reversed(range(10000))]

크기 10,000 부분 정렬된 랜덤 배열 (5위)

array = genRandomArray(size)
sorted_array = self.genSortedArray(size)
array[size // 4 : size // 2] = sorted_array[size // 4 : size // 2]
return array

 

big-O 계산기로 계산 결과

파이썬 정렬 알고리즘 big-O 시간 복잡도 계산하기

from bigO import bigO


def goSort(array):
    # Time Complexity O(nlogn) | Space Complexity O(1)
    def insertSort(array, begin=0, end=None):
        if end == None:
            end = len(array)
        for i in range(begin, end):
            j = i
            toChange = array[i]
            while j != begin and array[j - 1] > toChange:
                array[j] = array[j - 1]
                j -= 1
            array[j] = toChange
        return array

    def siftDown(array, lo, hi, first):
        root = lo
        while True:
            child = 2 * root + 1
            if child >= hi:
                break

            if child + 1 < hi and array[first + child] < array[first + child + 1]:
                child += 1

            if array[first + root] >= array[first + child]:
                return

            array[first + root], array[first + child] = (
                array[first + child],
                array[first + root],
            )
            root = child

    def heapSort(array, a, b):
        first = a
        lo = 0
        hi = b - a

        # Build heap with greatest element at top.
        for i in range((hi - 1) // 2, -1, -1):
            siftDown(array, i, hi, first)

        # Pop elements, largest first, into end of data.
        for i in range(hi - 1, -1, -1):
            array[first], array[first + i] = array[first + i], array[first]
            siftDown(array, lo, i, first)

    def unsigned(n):
        return n & 0xFFFFFFFF

    def medianOfThree(array, m1, m0, m2):
        # sort 3 elements
        if array[m1] < array[m0]:
            array[m1], array[m0] = array[m0], array[m1]

        # data[m0] <= data[m1]
        if array[m2] < array[m1]:
            array[m2], array[m1] = array[m1], array[m2]

            # data[m0] <= data[m2] && data[m1] < data[m2]
            if array[m1] < array[m0]:
                array[m1], array[m0] = array[m0], array[m1]

        # now data[m0] <= data[m1] <= data[m2]

    def doPivot(array, lo, hi):
        m = int(unsigned(lo + hi) >> 1)

        if hi - lo > 40:
            # Tukey's ``Ninther,'' median of three medians of three.
            s = (hi - lo) // 8
            medianOfThree(array, lo, lo + s, lo + 2 * s)
            medianOfThree(array, m, m - s, m + s)
            medianOfThree(array, hi - 1, hi - 1 - s, hi - 1 - 2 * s)

        medianOfThree(array, lo, m, hi - 1)

        pivot = lo
        a, c = lo + 1, hi - 1

        while a < c and array[a] < array[pivot]:
            a += 1
        b = a
        while True:
            while b < c and array[pivot] >= array[b]:
                b += 1
            while b < c and array[pivot] < array[c - 1]:
                c -= 1
            if b >= c:
                break

            array[b], array[c - 1] = array[c - 1], array[b]
            b += 1
            c -= 1

        protect = hi - c < 5
        if not protect and hi - c < (hi - lo) // 4:
            dups = 0
            if array[pivot] >= array[hi - 1]:
                array[c], array[hi - 1] = array[hi - 1], array[c]
                c += 1
                dups += 1
            if array[b - 1] >= array[pivot]:
                b -= 1
                dups += 1

            if array[m] >= array[pivot]:
                array[m], array[b - 1] = array[b - 1], array[m]
                b -= 1
                dups += 1

            protect = dups > 1

        if protect:
            while True:
                while a < b and array[b - 1] >= array[pivot]:
                    b -= 1
                while a < b and array[a] < array[pivot]:
                    a += 1
                if a >= b:
                    break

                array[a], array[b - 1] = array[b - 1], array[a]
                a += 1
                b -= 1

        array[pivot], array[b - 1] = array[b - 1], array[pivot]
        return b - 1, c

    def quickSort(array, a, b, maxDepth):
        while b - a > 12:  # Use ShellSort for slices <= 12 elements
            if maxDepth == 0:
                return heapSort(array, a, b)

            maxDepth -= 1
            mlo, mhi = doPivot(array, a, b)
            # Avoiding recursion on the larger subproblem guarantees
            # a stack depth of at most lg(b-a).
            if mlo - a < b - mhi:
                quickSort(array, a, mlo, maxDepth)
                a = mhi  # i.e., quickSort(array, mhi, b)
            else:
                quickSort(array, mhi, b, maxDepth)
                b = mlo  # i.e., quickSort(array, a, mlo)

        if b - a > 1:
            # Do ShellSort pass with gap 6
            # It could be written in this simplified form cause b-a <= 12
            for i in range(a + 6, b):
                if array[i] < array[i - 6]:
                    array[i], array[i - 6] = array[i - 6], array[i]

            return insertSort(array, a, b)

    maxDepth = 2 * (len(array).bit_length() - 1)
    quickSort(array, 0, len(array), maxDepth)
    return array


tester = bigO.bigO()
#complexity, _, res = tester.test(goSort, "random")

tester.test_all(goSort)

 

한줄평 : 모든 상황에서 quickSort보다 무난하게 빠르며, 나쁘지 않음