Python Fast inverse square root

고속 역 제곱근

Fast inverse square root - Wikipedia

(Fast inverse square root)

@wikipedia

 

1. 소개

IEEE 754 부동소수점 체계의 32비트 실수에 대한 제곱근의 역수를 계산하기 위한 알고리즘이다.- Wikipedia

= $1/\sqrt{x}$ 을 계산하기 위한 알고리즘 (bit-shift와 곱셈만으로 구할 수 있음)

(지금은 프로세서에서는 이 기법은 "fast"하지 않다. SSE rsqrt가 더 빠른 듯)

 

@wikipedia - 알고리즘 설명

 

어디서 주로 사용되냐면, 옛날 3D 그래픽 게임에서 조명 처리와 같은 연산에 입사각과 반사각을 계산할 때

고속 역 제곱근 알고리즘을 사용했다.

(3D 게임에선 같은 연산을 수십억, 수조억 번 반복할 수 있는데, "minor" 하지만, 연산 방법을

조금이라도 최적화를 시키면 성능 향상에 큰 도움이 된다.)

 

아래는 실제로 Quake 3 Arena 코드에서 사용된 고속 역 제곱근 소스이다. (주석만 변경함)

float Q_rsqrt( float number )
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;

	x2 = number * 0.5F;
	y = number;
	i = * ( long * ) &y;  // store floating-point bits in integer
	i = 0x5f3759df - ( i >> 1 );  // initial guess for Newton's method
	y = * ( float * ) &i;  // convert new bits into float
	y = y * ( threehalfs - ( x2 * y * y ) );  // One round of Newton's method
//	y = y * ( threehalfs - ( x2 * y * y ) );  // 2nd round of Newton's method, this can be removed
	// 뉴턴 법을 반복할 수록 정확도가 올라감
    
	return y;
}

 

2. 뉴턴 방법

뉴턴 방법이란 실숫값 함수의 영점을 근사하는 방법의 하나이다.

(모든 함수의 루트 근사 값을 구할 수 있는 방법)

뉴턴 방법은 "좋은" 추측으로 값이 달라질 수 있는데, 자세한 내용은 위키백과 참고

아래는 뉴턴 방법을 이용해, $1/\sqrt{n}$ 이 ($\sqrt{n}$ ~$~n/2$) 중간 값이라고 생각했을 때 결과이다.

n에 2, 4, 10..등 대입해보자.

 

 

3. 매직 넘버 0x5F3759DF

mantissa(기수) 계산을 할 때 오류를 보정하기 위한 수라고 하는데,

예를 들면, float to int란 함수에서

int float_to_int(float f) {
  return *(int*)&f;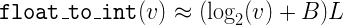
}

L = 2^23

위와 같은 결과가 나오고,

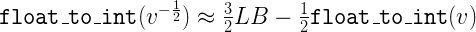
위와 같이 나와서, 

라는 결과가 나오는데, log2의 정확도를 올리기 위해, 좀 더 작은 값을 선택해서 

0x5F3759DF가 나온다...라는 이야기인데 자세한 설명은 아래 사이트를 참고 (수학)

h14s.p5r.org/2012/09/0x5f3759df.html

 

4. 파이썬

(파이썬에서 32비트, 64비트 float이란 메모리 느낌이 강하다.)

from struct import pack, unpack


def sqrt2(num):
    threehalfs = 1.5
    x2 = num * 0.5
    y = num

    packed_y = pack("f", y)
    i = unpack("i", packed_y)[0]  # treat float's bytes as int
    i = 0X5F3759DF - (i >> 1)  # arithmetic with magic number
    # 혹은 0x5F375A86
    packed_i = pack("i", i)
    y = unpack("f", packed_i)[0]  # treat int's bytes as float

    y = y * (threehalfs - (x2 * y * y))  # Newton's method
    y = y * (threehalfs - (x2 * y * y))  # 2nd, Newton's method
    return y * num

if __name__ == "__main__":

    print(sqrt2(2))
    print(sqrt2(8))
    print(sqrt2(25))
    print(sqrt2(100))
    
''' 결과

1.4142134292714543  # 실제 1.414213562373095
2.8284268585429087  # 실제 2.82842712474619
4.9999819350525465  # 실제 5.0
9.999963870105093  # 실제 10.0
'''

 

벤치마킹 math.sqrt vs FIS

from timeit import timeit


if __name__ == "__main__":
    start = default_timer()
    for i in range(1, 10000):
        sqrt(i)
    print(f"Execution Time on math.sqrt: {default_timer() - start:.5f}s")

    start = default_timer()
    for i in range(1, 10000):
        sqrt2(i)
    print(f"Execution Time on sqrt2: {default_timer() - start:.5f}s")
    
''' 결과

Execution Time on math.sqrt: 0.00190s

Execution Time on sqrt2: 0.01297s

'''

 

참고

0x5F3759DF에 대한 자세한 수학적 설명

Understanding of Quake's Fast Inverse Square Root

위키피디아 (Fast inverse square root)

Fast inverse square root - Wikipedia